
R - čtvercový vzorec (obsah)
- R - čtvercový vzorec
- Příklady R - čtvercový vzorec (se šablonou Excel)
- R - čtvercová kalkulačka
R - čtvercový vzorec
Vzorec R-kvadrát je také známý jako koeficient určení, je to statistické měřítko, které určuje korelaci mezi výkonem investora a výnosem nebo výkonem referenčního indexu. V zásadě ukazuje, do jaké míry lze výkonnost akcií nebo portfolií připsat konkrétnímu referenčnímu indexu. Tento vzorec je mírně odlišný od korelace proměnné, protože korelační vzorec ukazuje vztah mezi závislou a nezávislou proměnnou, zatímco na druhé straně R -svazovaný vzorec ukazuje, do jaké míry rozptyl jedné proměnné vysvětluje rozptyl druhé proměnné. .
Vzorec pro R - Squared je dán:
R – Squared = 1 – (Sum of First Errors / Sum of Second Errors)
Příklady R - čtvercový vzorec (se šablonou Excel)
Vezměme si příklad, abychom lépe porozuměli výpočtu R - Squared.
Tuto šablonu vzorců R - Squared si můžete stáhnout zde - R - Squared Formula TemplatePříklad č. 1
Zvažte následující informace a vypočítejte R na druhou.
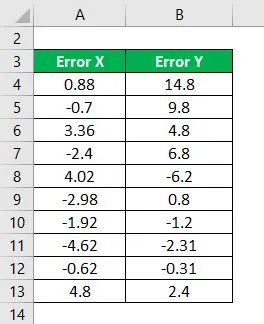
Čtverec chyby X se vypočte jako:
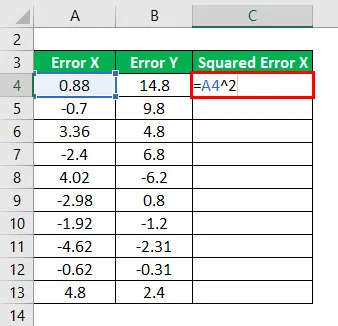
Výsledek bude uveden níže.
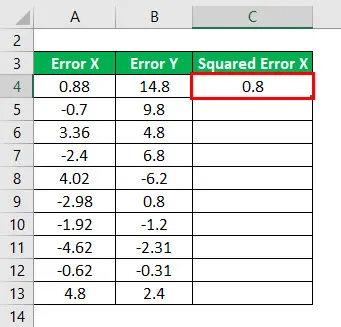
Čtverec chyby X pro všechna data, jak je uvedeno níže.
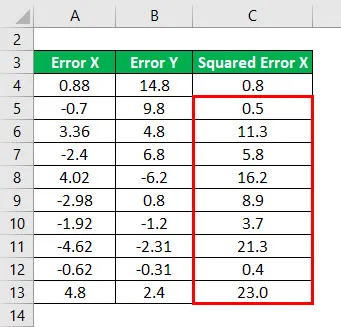
Podobně musíme pro všechna data vypočítat druhou mocninu Y.
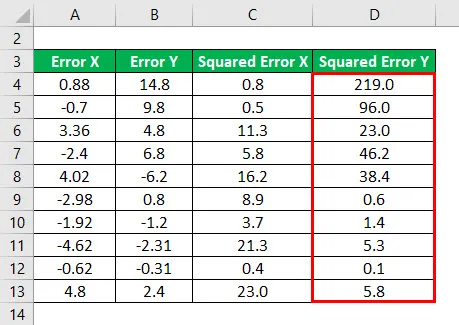
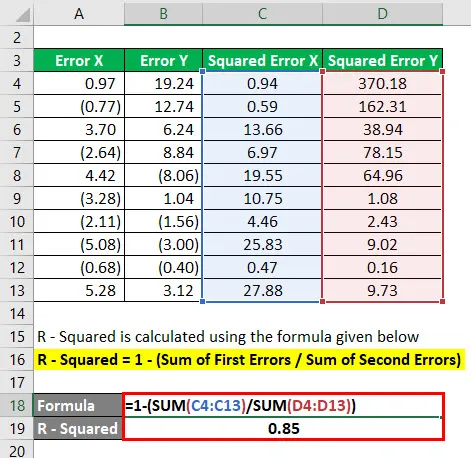
R - Squared se vypočítá pomocí vzorce uvedeného níže
R - na druhou = 1 - (součet prvních chyb / součet druhých chyb)
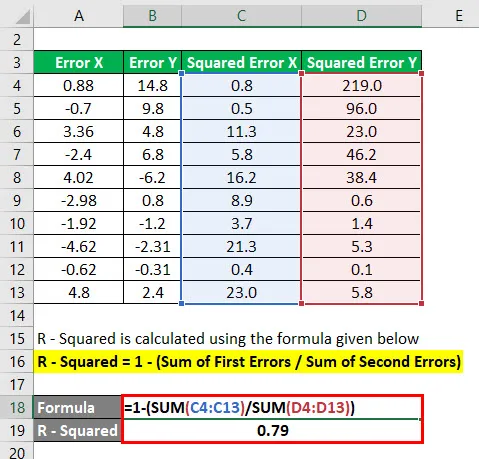
Zde nejprve jsme na druhou mocninu chyby následujících bodů a provedli shrnutí výše uvedených problémů. Poté se součet první chyby vydělí součtem druhé chyby a odečte se 1.
R-kvadrát leží v rozmezí 0 až 1. Hodnota r-s vypnutá 1 nebo 100% znamená, že všechny pohyby v indexu jsou zcela vysvětleny pohyby v referenčním indexu.
Příklad č. 2
Zvažte následující informace a vypočítejte R na druhou.
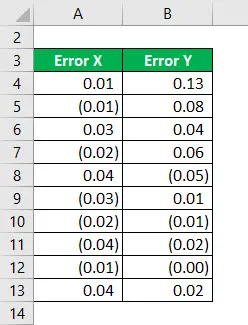
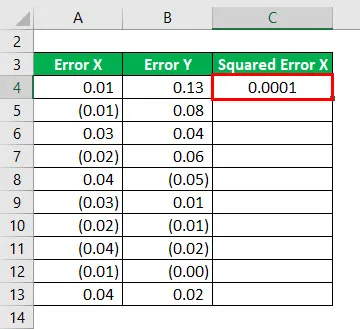
Čtverec chyby X se vypočte jako:
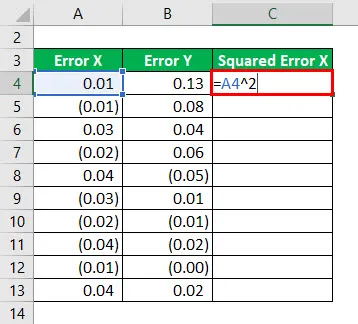
Výsledek bude uveden níže.
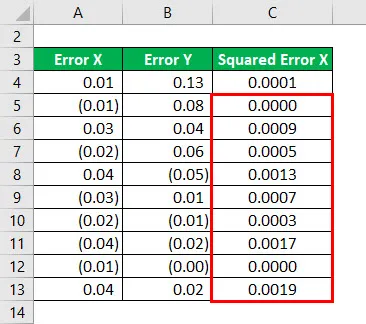
Druhá mocnina chyby X pro všechna data uvedená níže.
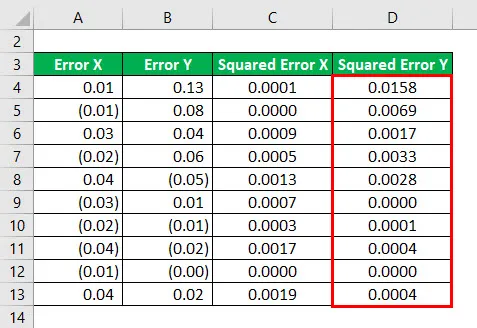
Podobně musíme vypočítat druhou mocninu chyby Y pro všechna data.
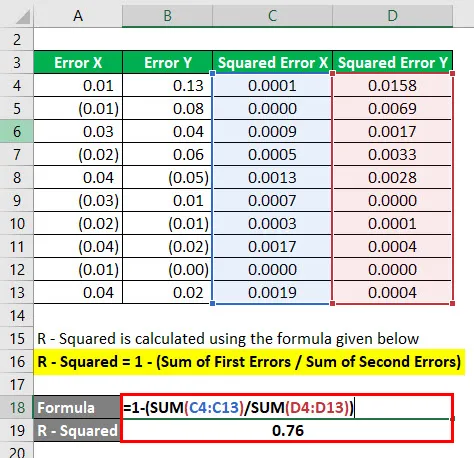
R - Squared se vypočítá pomocí vzorce uvedeného níže
R - na druhou = 1 - (součet prvních chyb / součet druhých chyb)
Příklad č. 3
Zvažte následující informace a vypočítejte R na druhou.
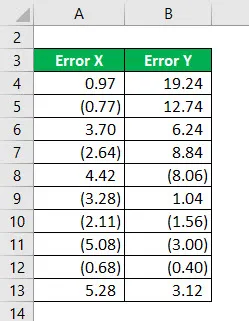
Druhá mocnina chyby X se vypočte jako:
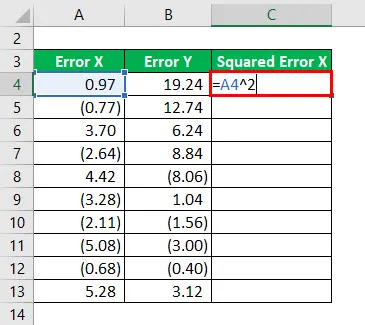
Výsledek bude uveden níže.
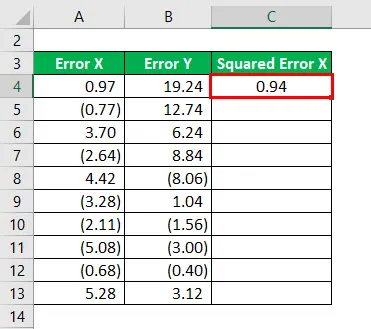
Druhá mocnina chyby X pro všechna data uvedená níže.
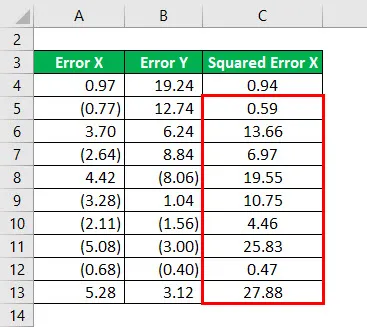
Podobně musíme vypočítat druhou mocninu chyby Y pro všechna data.
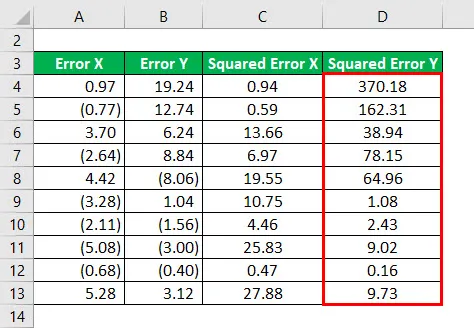
R - Squared se vypočítá pomocí vzorce uvedeného níže
R - na druhou = 1 - (součet prvních chyb / součet druhých chyb)
Relevance a použití
- Tento vzorec je široce používán správci portfolia a správci fondů jako měřítko, které říká, jak pohyby fondů korelují s benchmarkovým indexem.
- Tento vzorec se také používá v průmyslu na akciových trzích, který sděluje makléři nebo investorovi, jak dobře akcie korelují s celkovým pohybem trhu.
- Tento vzorec má svá vlastní omezení, protože nemůže posoudit, zda jsou odhady koeficientů a předpovědi zkreslené či nikoli, stačí posoudit zbývající grafy.
- Tam, kde R - Squared neslouží jako dobrý srovnávací model pro srovnání dobrého stavu dvou proměnných, je R-Squared upravený většinou používán k provádění více lineárních regresí.
- Nízké nebo vysoké R- na druhou mocninu nemůže být vždy dobré nebo špatné, protože to uživateli neřekne spolehlivost modelu.
- Pokud má uživatel nízkou hodnotu na druhou mocninu, ale nezávislé proměnné jsou statisticky významné, může si uživatel stále vyvodit důležité závěry o vztazích mezi proměnnými.
R - čtvercová kalkulačka
Můžete použít následující kalkulačku R - Squared
| Součet prvních chyb | |
| Součet druhých chyb | |
| R - čtvercový vzorec | |
| R - čtvercový vzorec | 1 - (Součet prvních chyb / Součet druhých chyb) |
| = | 1 - (0/0) = 0 |
Doporučené články
Toto byl průvodce R - Squared Formula. Zde diskutujeme, jak spočítat R - Squared spolu s praktickými příklady. Rovněž poskytujeme kalkulačku R - Squared se šablonou Excel ke stažení. Další informace naleznete také v následujících článcích -
- Průvodce očekávaným vzorcem návratu
- Jak vypočítat poměr PEG?
- Příklady vzorce solventnosti
- Kalkulačka pro výpočet pákového poměru