Excel NORMSINV (obsah)
- Úvod do Excelu NORMSINV
- Jak používat NORMSINV Formula v Excelu?
Úvod do Excelu NORMSINV
Funkce inverzní normální kumulativní distribuce ve Excelu je důležitým nástrojem, který vrací inverzní normální kumulativní distribuci pro danou hodnotu pravděpodobnosti, tj. Obvykle vrací inverzní hodnotu standardní normální kumulativní distribuce (která má střední hodnotu nula a směrodatnou odchylku jedna) Funkce NORM.S.INV je poprvé představena v Microsoft Excel verze 2010, což je aktualizovaná verze funkce NORMSINV v Excelu 2013 a nejnovější verzi. Funkce NORMSINV se nejčastěji používá v analýze závazků a financí.
Syntaxe Excel NORMSINV

Argument:
Pravděpodobnost - Což není nic jiného než pravděpodobnost odpovídá normálnímu rozdělení.
Jak používat NORMSINV Formula v Excelu?
V Microsoft Excelu je zabudovaná funkce NORMSINV roztříděna do statistické funkce, která je zobrazena na níže uvedeném snímku obrazovky (kde vypočítá inverzní hodnotu normálního kumulativního rozdělení pro danou pravděpodobnost).
- Přejděte do nabídky Vzorce.
- Klikněte na Další funkce, jak je uvedeno na níže uvedeném snímku obrazovky.

- Vyberte statistickou kategorii, pod níž najdeme funkci NORM.DIST, jak je ukázáno níže.
Příklad č. 1 - Použití NORM.DIST a NORMSINV
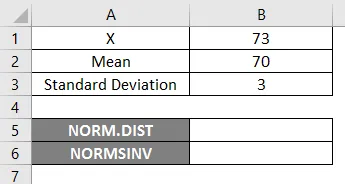
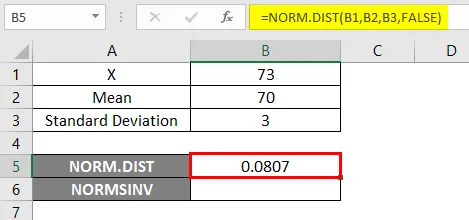
Abychom mohli používat funkci NORM.DIST, začněme snadným příkladem, kde potřebujeme zjistit studentské známky, předpokládejme, že máme třídní zkoušku s průměrným hodnocením 70 tj. Mu = 70 a standardní směrodatná odchylka je 3 body, tj. Sigma = 3 Zde musíme zjistit, jaká je pravděpodobnost, že studenti získali známky 73 nebo nižší, tj. P (X <= 73). Podívejme se tedy, jak zjistit pravděpodobnost pomocí funkce NORM.DIST.
- X = 3
- Průměr = 70
- Standardní odchylka = 3
- Použijte funkci NORM.DIST níže.
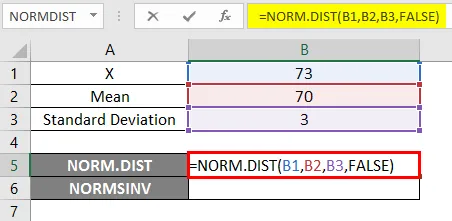
- Pokud použijeme výše uvedenou funkci NORM.DIST, dostaneme pravděpodobnost 0, 0807.
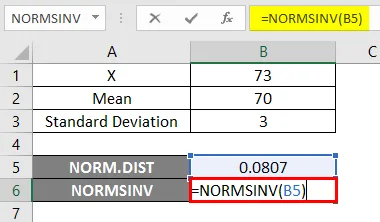
- Nyní použijte funkci NORMSINV k nalezení inverze k normálnímu kumulativnímu rozdělení, jak je ukázáno níže.
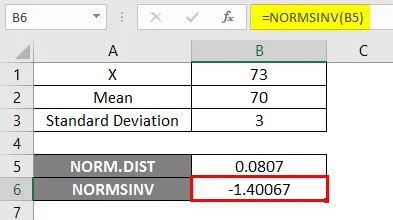
Výsledek -
Ve výsledku níže vidíme, že jsme dostali negativní hodnoty -1 40067 pro danou pravděpodobnost, tj. Inverzní normální kumulativní distribuci.
Příklad č. 2 - Průměrná a přesná směrodatná odchylka
Podívejme se na další příklad s daty založenými na křivkách, abychom mohli poznat střední a přesnou směrodatnou odchylku.
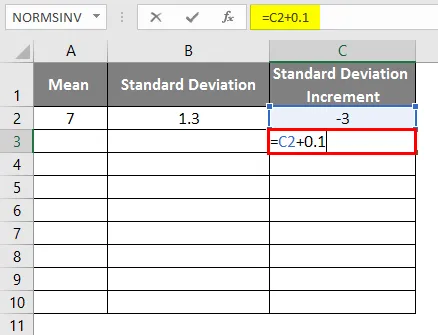
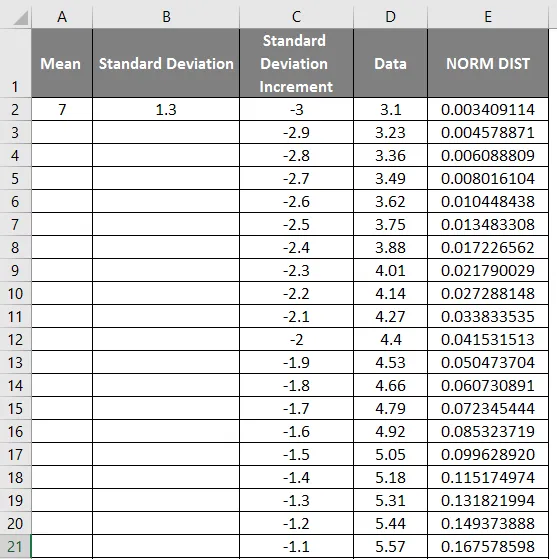
- Průměr = 7
- Standardní odchylka = 1, 3
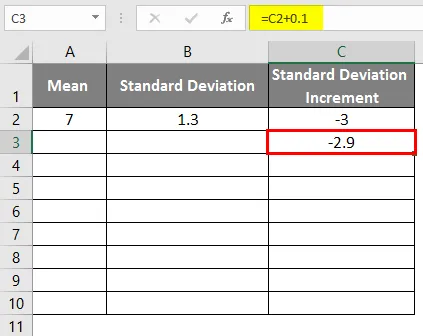
- Standardní odchylka odchylky jako -3

- Abychom dostali zvonovou křivku, musíme přidat 0, 1 ke standardnímu přírůstku odchylky, kde jsou data níže.
- Po použití vzorce je výsledek uveden níže.
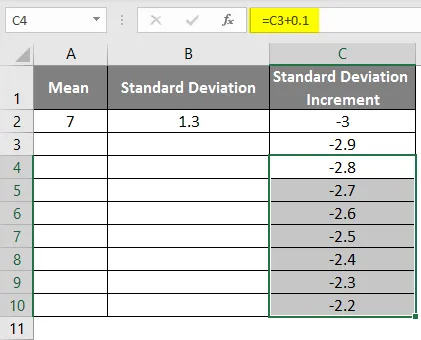
- Přetažením hodnot získáte více hodnot, dokud nedostaneme kladné hodnoty, abychom dostali levou křivku.
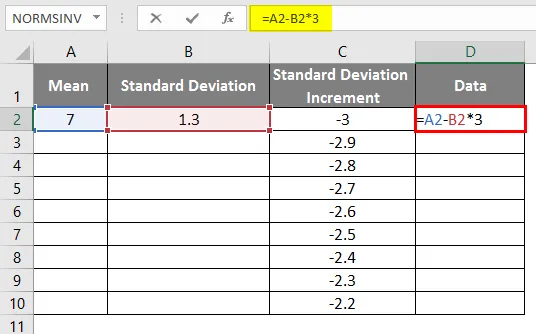
- Abychom dostali správnou křivku, musíme použít vzorec jako = střední standardní odchylka * 3, abychom dostali přesné křivky.
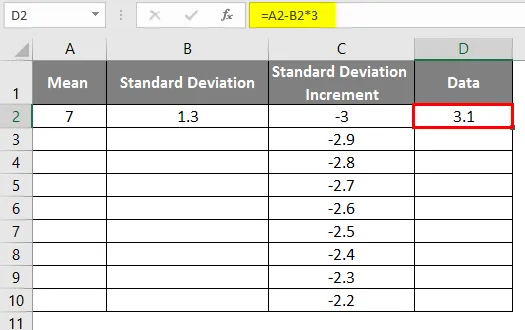
- Po použití vzorce je výsledek uveden níže.
- Stejně jako ve výše uvedených datech pro standardní odchylku odchylky pro získání levé křivky jsme hodnoty zvýšili o 0, 1
- Stejný scénář se používá při použití vzorce jako = 3.1 + STANDARD DEVIATION / 10, aby se přírůstek křivky 0, 1
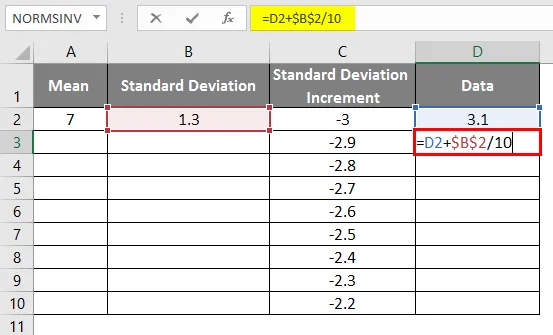
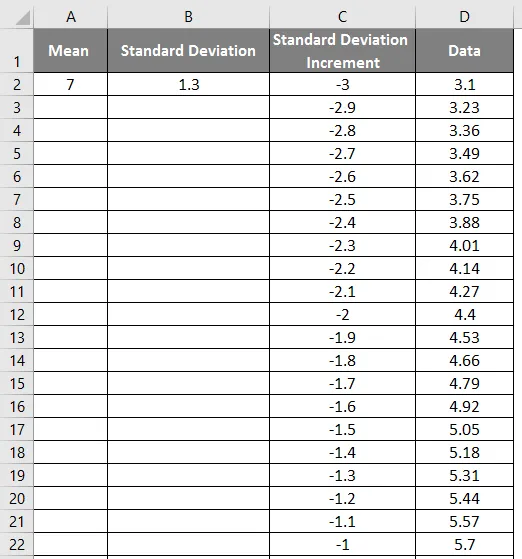
- Po použití vzorce je výsledek uveden níže.

- Přetažením hodnot získáte přesný výsledek, který je zobrazen na níže uvedeném snímku obrazovky.
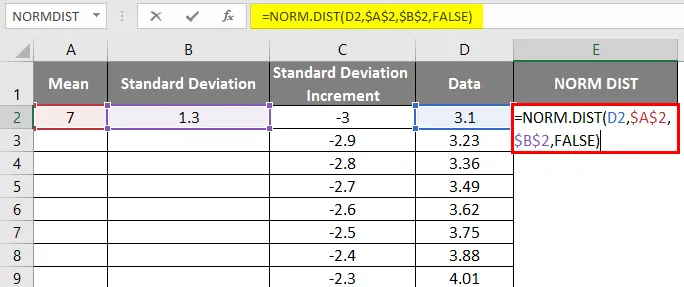
- Nyní použijte normální distribuční funkci pomocí vzorce = NORM.DIST (hodnota DATA, průměr, směrodatná odchylka, false).
- Níže uvedený výsledek získáme následovně.
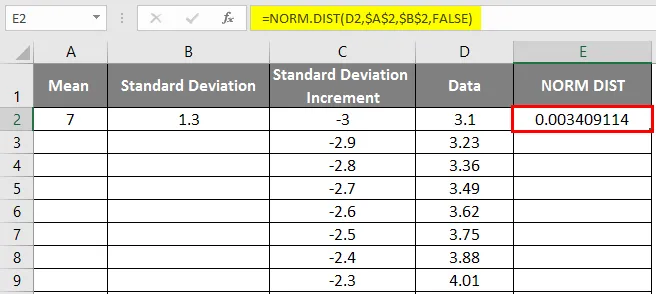
- Přetažením hodnot získáte přesný výsledek, který je uveden níže.
- Jak je vidět na obrázku výše, vypočítali jsme NORMÁLNÍ rozdělení z průměrné a standardní odchylky. Nyní se podívejme, co bude inverzní k NORMÁLNÍ distribuci použitím NORMSINV, který je uveden níže.
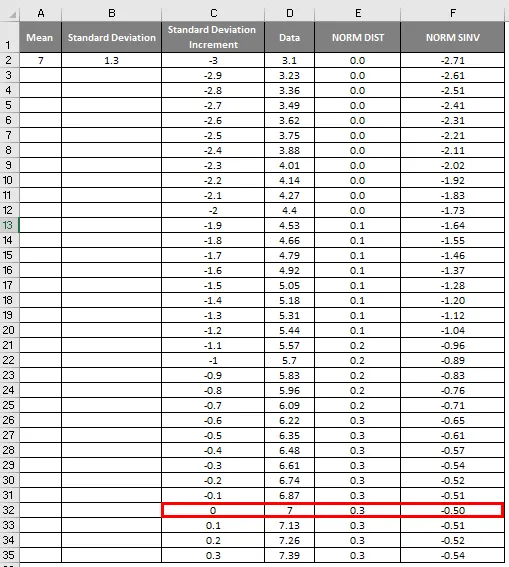
- Zde vidíme, že hodnota Zero (0) má standardní odchylku 7.

Pomocí rozptýleného grafu se podíváte, jak se objeví levá a pravá křivka.
- Nejprve vyberte data a sloupec Normální.
- Přejděte na kartu Vložit a vyberte rozptýlený graf následujícím způsobem.
- Získáme graf křivky níže, jak je znázorněno níže.
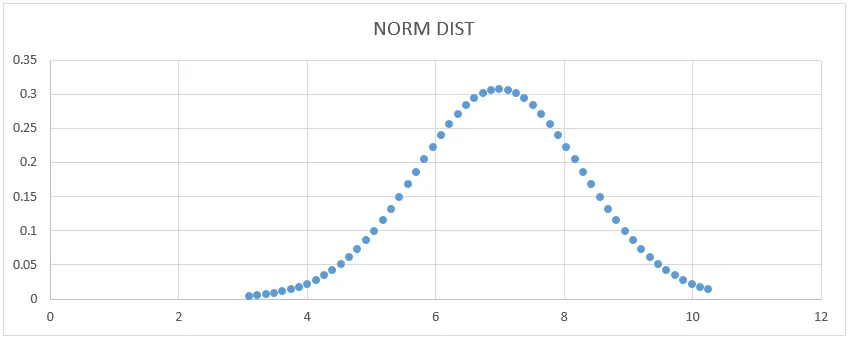
Zde vidíme, že střední hodnota 7 má standardní tvar odchylky, kde můžeme ukázat, že nakreslením přímky ji reprezentujeme.
- Průměr = 7
- 1 - standardní odchylka označuje 68% dat.
- 2 - standardní odchylka označuje 95% dat.
- 3 - standardní odchylka označuje 99, 7% dat.
Normální distribuční graf:
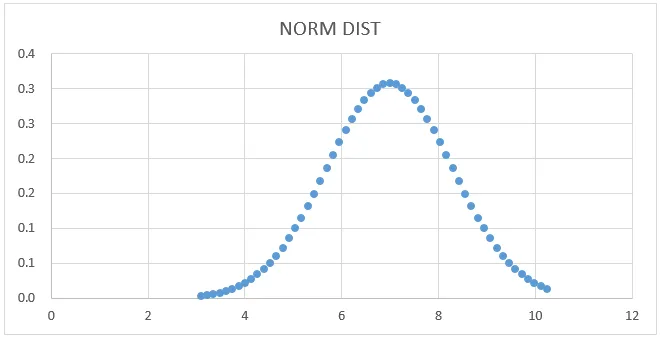
Graf NORMSINV:
Nyní z výše uvedeného obrázku vyberte sloupec dat a NORM SINV, abyste získali níže uvedený graf.
- Nejprve vyberte data a sloupec Normální.
- Přejděte na kartu Vložit a vyberte rozptýlený graf.
- Dostaneme níže uvedený graf, který je zobrazen na níže uvedeném snímku obrazovky.
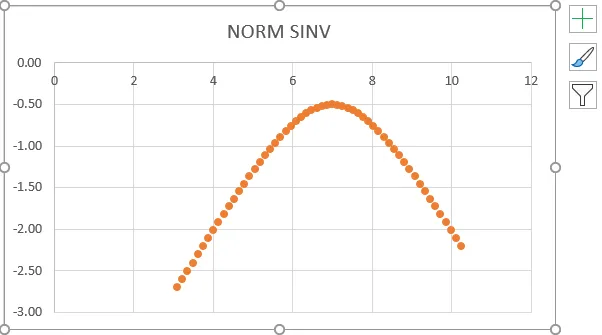
- Z výše uvedeného snímku můžeme vidět, že jsme dostali přesný inverzní signál k normální distribuci, která ukazuje stejnou hodnotu hodnoty uvedenou níže.

Příklad č. 3 - Konfigurace levé a pravé křivky
V tomto příkladu nakonfigurujeme levou a pravou křivku pomocí funkce normální distribuce. Zvažte níže uvedená data, jak je uvedeno níže, kde x má záporné hodnoty a zvyšuje se na kladné hodnoty.
- Použijte vzorec = NORM.DIST (A2, 0, 1, 1).
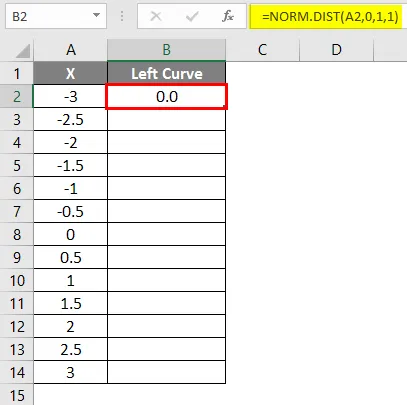
- Po použití vzorce je výsledek uveden níže.
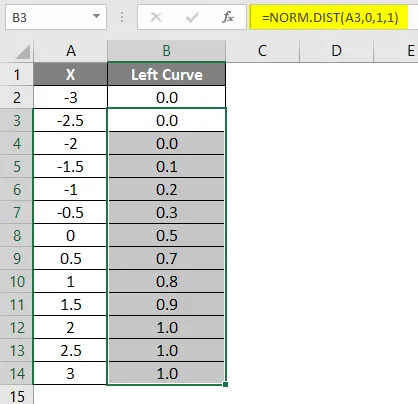
- Přetáhněte vzorec do jiných buněk.
- Použijte vzorec = 1-B2 .
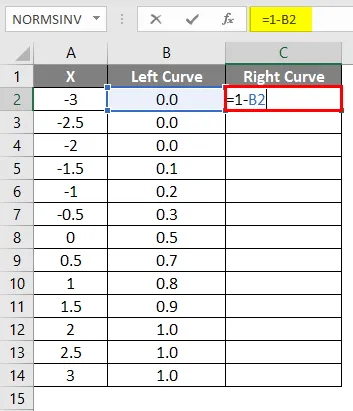
- Po použití vzorce je výsledek uveden níže.
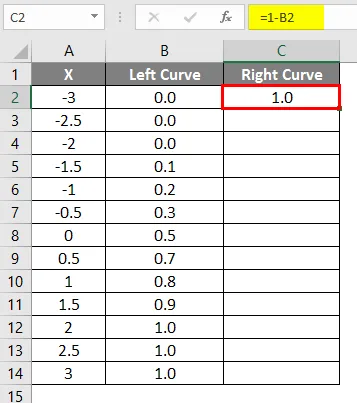
- Přetáhněte stejný vzorec do jiných buněk.
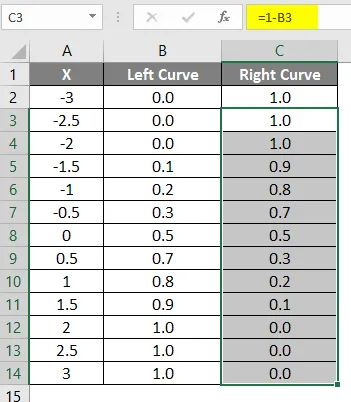
Výsledek výše uvedeného vzorce je uveden níže.
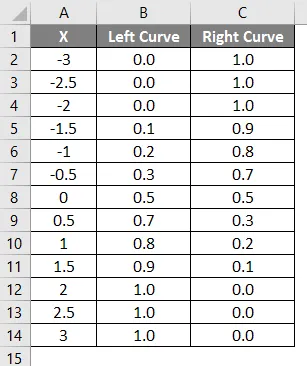
- Hodnoty levých křivek byly vypočteny pomocí vzorce NORMÁLNÍ DISTRIBUCE nastavením kumulativní hodnoty jako True a hodnota NORMSINV byla vypočtena pomocí levé křivky.
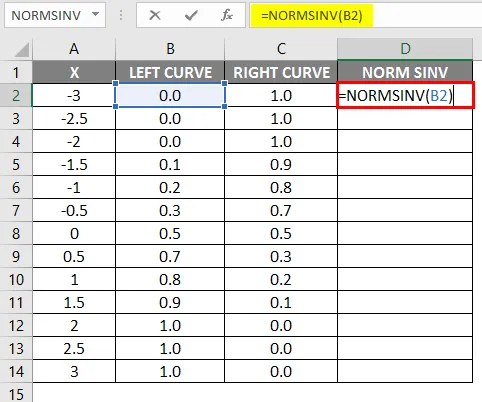
- Po použití vzorce je výsledek uveden níže.
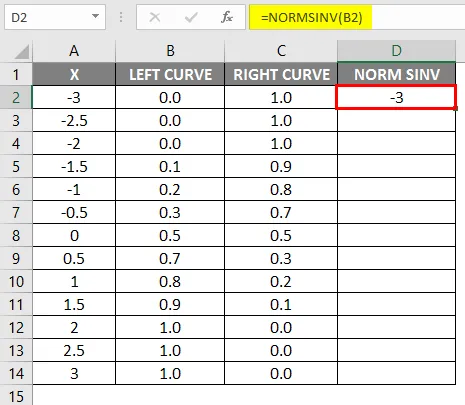
- Přetáhněte stejný vzorec do jiných buněk.
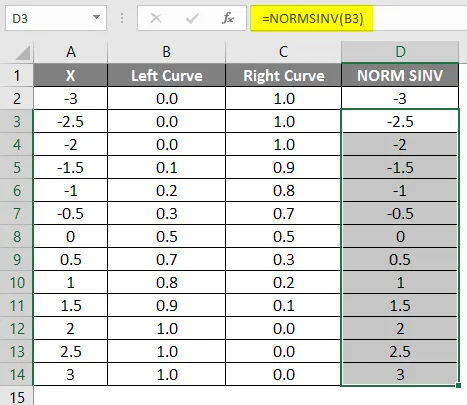
Jak vidíme, dostali jsme stejnou hodnotu pro NORMSINV, což není nic jiného než inverze normální distribuce. Stejným způsobem získáme správnou hodnotu křivky výpočtem hodnoty 1 křivky vlevo. V dalším kroku se pomocí rozptýleného grafu zkontrolujeme, jak dosáhneme výšky x.
- Vyberte sloupec nalevo a pravou křivku.
- Přejít na vložení nabídky.
- Vyberte rozptýlený graf následujícím způsobem.
Získáme výsledek níže uvedeného grafu, jak je znázorněno níže.
Graf NORM SINV:
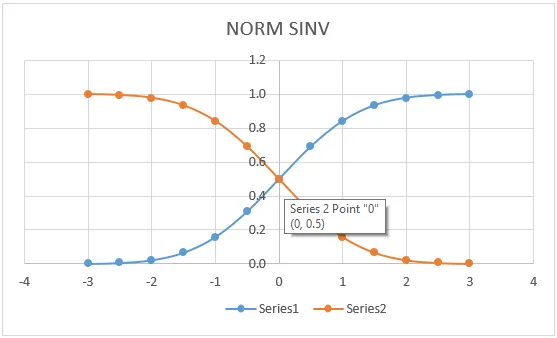
V níže uvedeném grafu vidíme, že křivka hodnoty NORM DISTRIBUTION má přesnou shodu pro (0, 0, 5), která leží ve středu čáry, kde dostaneme stejný graf, pokud se ucházíme o NORMDIST.
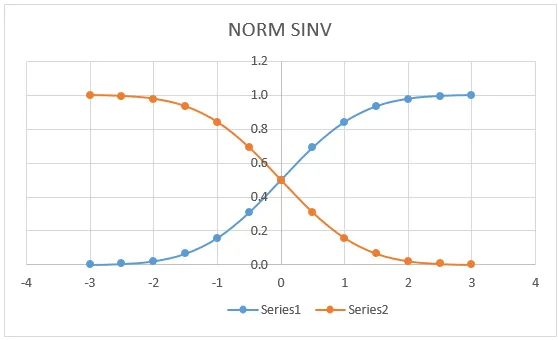
Zde ve výše uvedeném grafu velmi jasně ukazuje, že přesný průměr jsme dostali ve středu, který označuje:
- X = 0
- Levá křivka = 0, 5
- Pravá křivka = 0, 5
Zobrazili jsme ji pro zobrazení hodnot NORMSINV v grafickém formátu, jak je ukázáno níže.
Důležité informace o Excelu NORMSINV
- #hodnota! K chybě dochází, když je daný argument nečíselný nebo logický.
- Ve funkci normální distribuce obvykle dostaneme #NUM! chyba kvůli argumentu standardní odchylky je menší nebo rovna nule.
Doporučené články
Toto je průvodce Excel NORMSINV. Zde diskutujeme o tom, jak používat NORMSINV v Excelu spolu s praktickými příklady a šablonou Excel ke stažení. Můžete si také prohlédnout naše další doporučené články -
- Jak používat jméno v Excelu?
- Práce s Matrixem v Excelu
- Co když analýza v Excelu
- Vzorec NPV v Excelu