Kvartilní odchylka vzorce Kalkulačka (příklady se šablonou Excelu)

• Co je Quartile Deviation Formula?

Kvartilní odchylka vzorce (obsah)

• Vzorec
• Příklady
• Kalkulačka

Co je Quartile Deviation Formula?

Kvartilní odchylka (QD) je výsledkem poloviny rozdílu mezi horním a dolním kvartilem. Matematicky můžeme definovat jako:

Quartile Deviation = (Q 3 – Q 1 ) / 2

Kvartilní odchylka definuje absolutní míru rozptylu. Vzhledem k tomu, že relativní míra odpovídající QD je známa jako koeficient QD, který se získá použitím určitého souboru vzorců:

Coefficient of Quartile Deviation = (Q 3 – Q 1 ) / (Q 3 + Q 1 )

Koeficient QD se používá ke studiu a porovnání stupně variace v různých situacích.

Příklady vzorce kvartilních odchylek (se šablonou Excel)

Vezměme si příklad, abychom lépe porozuměli výpočtu vzorce Kvartilní odchylka.

Tuto šablonu Excel Quartile Deviation Formula si můžete stáhnout zde - šablonu Excel Quartile Deviation Formula

Vzorec kvartilové odchylky - příklad č. 1

Počet stížností podaných proti krádeži vozidel za den byl vypočítán pro následujících 10 dní. A data jsou uvedena níže. Vypočítejte kvartilní odchylku a její koeficient pro daný případ diskrétní distribuce.

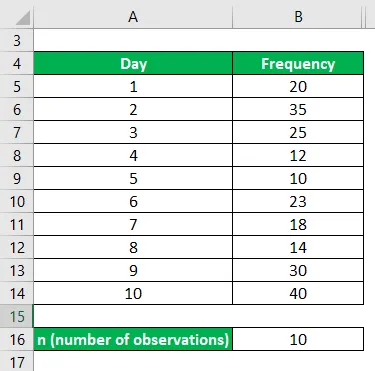
Řešení:

Uspořádat data ve vzestupném pořadí

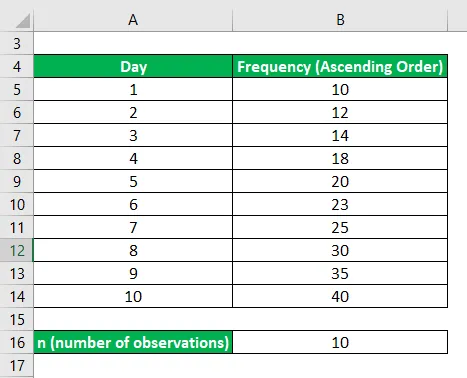
Nyní najdeme první kvartil, způsob, jakým leží na půli cesty mezi nejnižší hodnotou a střední hodnotou; kde třetí kvartil leží na půli cesty mezi střední a největší hodnotou.

První kvartil (Q ₁ ) se vypočítá pomocí vzorce uvedeného níže

První kvartil (Q ₁ )

Q _i = (i * (n + 1) / 4) ^té pozorování

Q ₁ = (1 * (10 + 1) / 4) ^té pozorování

Q ₁ = (1 * (10 + 1) / 4) ^té pozorování

Q ₁ = 2, 75. Pozorování

2.75. pozorování tedy leží mezi ^2. a 3. hodnotou v uspořádané skupině nebo uprostřed mezi 12 a 14

První kvartil (Q ₁ ) se vypočítá jako

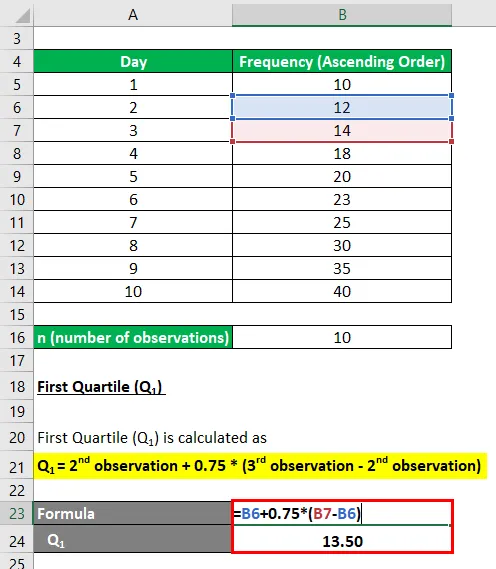
• Q ₁ = ^2. pozorování + 0, 75 * (3. pozorování - ^2. pozorování)
• Q ₁ = 12 + 0, 75 * (14 - 12)
• Q ₁ = 12 + 1, 50
• Q ₁ = 13, 50

Třetí kvartil (Q ₃ ) se vypočítá pomocí vzorce uvedeného níže

Třetí kvartil (Q ₃ )

Q _i = (i * (n + 1) / 4) ^thé obsevace

• Q ₃ = (1 * (n + 1) / 4) ^tého observace
• Q ₃ = ((10 + 1) / 4) ^thé obsevace
• Q ₃ = 8, 25. Pozorování

8..25. Pozorování tedy leží mezi 8. a 9. hodnotou v uspořádané skupině nebo uprostřed mezi 30 a 35

Třetí kvartil (Q ₃ ) se počítá jako

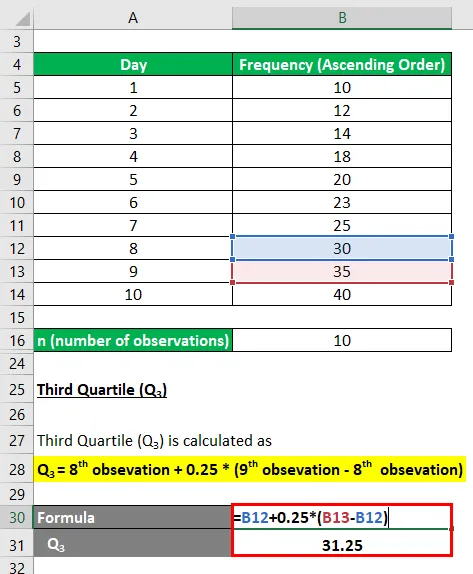
• Q ₃ = 8. observace + 0, 25 * (9. observace - 8. observace)
• Q ₃ = 30 + 0, 25 * (35 - 30)
• Q3 = 31, 25

Nyní pomocí kvartilních hodnot Q1 a Q3 vypočítáme jeho kvartilovou odchylku a její koeficient následujícím způsobem -

Kvartilní odchylka se vypočítá pomocí vzorce uvedeného níže

Kvartilní odchylka = (Q ₃ - Q ₁ ) / 2

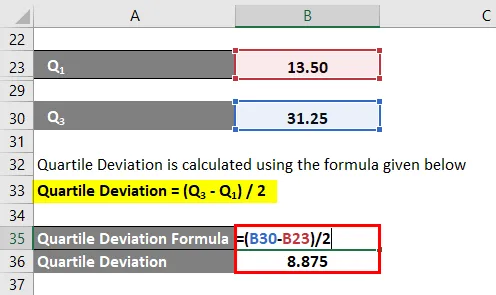
• Kvartilní odchylka = (31, 25 - 13, 50) / 2
• Kvartilní odchylka = 8, 875

Koeficient kvartilní odchylky se vypočítá pomocí vzorce uvedeného níže

Koeficient kvartilní odchylky = (Q ₃ - Q ₁ ) / (Q ₃ + Q ₁ )

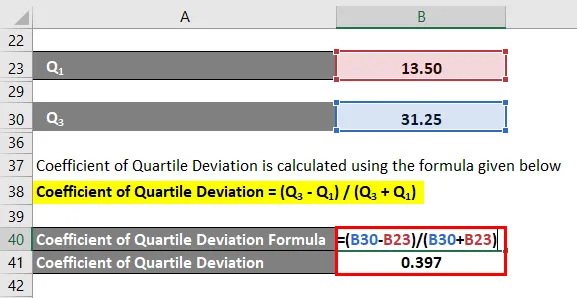
• Koeficient kvartilní odchylky = (31, 25 - 13, 50) /(31, 25 + 13, 50)
• Koeficient kvartilní odchylky = 0, 397

Kvartilní odchylka vzorce - Příklad č. 2

Následuje pozorování, které ukazuje jednodenní prodej nákupního centra, kde určujeme frekvenci prvních 50 zákazníků různé věkové skupiny. Nyní musíme vypočítat kvartilní odchylku a koeficient kvartilní odchylky.

Řešení:

V případě distribuce frekvence lze kvartily vypočítat pomocí vzorce:

Q _i = l + (h / f) * (i * (N / 4) - c) ; i = 1, 2, 3

Kde,

• l = Dolní hranice kvartilové skupiny
• h = šířka kvartilové skupiny
• f = Frekvence kvartilové skupiny
• N = celkový počet pozorování
• c = kumulativní frekvence

Nejprve musíme vypočítat kumulativní frekvenční tabulku

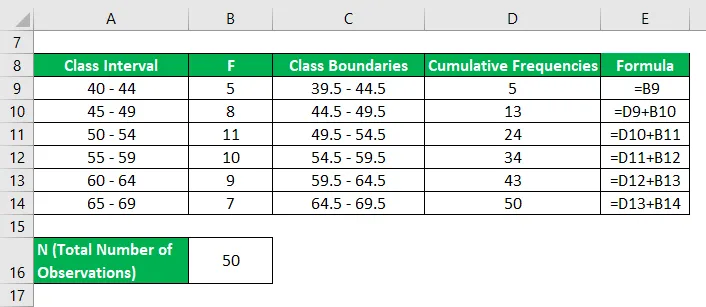
První kvartil (Q ₁ ) se vypočítá pomocí vzorce uvedeného níže

První kvartil (Q ₁ )

Q _i = (i * (N) / 4) ^thé obsevace

• Q ₁ = (1 * (50) / 4) ^thé obsevace
• Q ₁ = 12, 50. Obsevace

Od 12.50 je hodnota v intervalu 44, 5 - 49, 5

Proto skupina Q1 je (44, 5 - 49, 5)

Q _i = l + (h / f) * (i * (N / 4) - c)

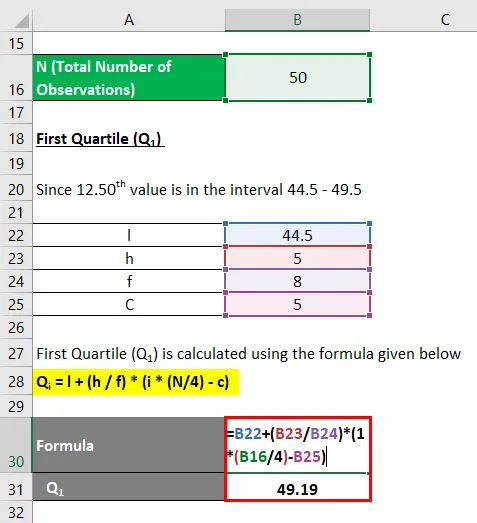
• Q ₁ = (44, 5 + (5/8) * (1 * (50/4) - 5)

• Q ₁ = 44, 5 + 4, 66875
• Q ₁ = 49, 19

Třetí kvartil (Q ₃ ) se vypočítá pomocí vzorce uvedeného níže

Třetí kvartil (Q ₃ )

Q _i = (i * (N) / 4) ^thé obsevace

Q1 = (i * (N) / 4) ^thé obsevace

• Q ₃ = (3 * (50) / 4) ^thé obsevace
• Q ₃ = 37, 50. Obsevace

Protože 37, 50. Hodnota je v intervalu (59, 5 - 64, 5)

Proto skupina Q3 je (59, 5 - 64, 5)

Q _i = l + (h / f) * (i * (N / 4) - c)

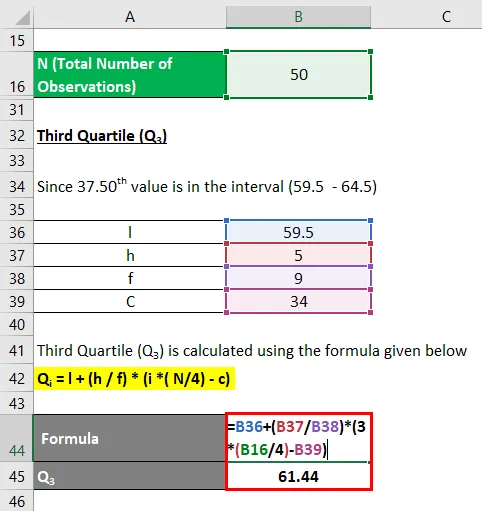
• Q3 = 59, 5 + (5/9) * (3 * (50/4) - 34)

• Q3 = 59, 5 + 1, 944

• Q3 = 61, 44

Vložením hodnot do vzorců kvartilové odchylky a koeficientu kvartilové odchylky dostaneme:

Kvartilní odchylka se vypočítá pomocí vzorce uvedeného níže

Kvartilní odchylka = (Q ₃ - Q ₁ ) / 2

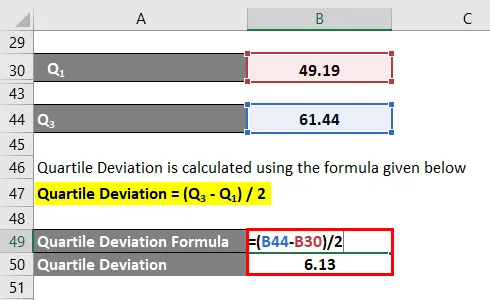
• Kvartilní odchylka = (61, 44 - 49, 19) / 2
• Kvartilní odchylka = 6.13

Koeficient kvartilní odchylky se vypočítá pomocí vzorce uvedeného níže

Koeficient kvartilní odchylky = (Q ₃ - Q ₁ ) / (Q ₃ + Q ₁ )

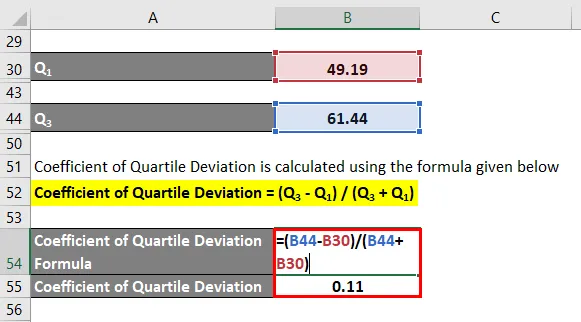
• Koeficient kvartilní odchylky = (61, 44 - 49, 19) / (61, 44 + 49, 19)
• Koeficient kvartilové odchylky = 12, 25 / 110, 63
• Koeficient kvartilové odchylky = 0, 11

Vysvětlení

Kvartilní odchylka je rozptyl uprostřed dat, kde definuje šíření dat. Jak víme, že rozdíl mezi třetím kvartilem a prvním kvartilem se nazývá mezikvartilový rozsah a polovina mezikvartilového rozsahu se nazývá polokapartil, který se také nazývá kvartilní odchylka. Nyní můžeme vypočítat odchylku kvartilu pro seskupená i neseskupená data pomocí vzorce uvedeného níže.

Kvartilní odchylka = (třetí kvartil - první kvartil) / 2

Kvartilní odchylka = (Q ₃ - Q ₁ ) / 2

Zatímco koeficient kvartilní odchylky je používán pro srovnání variace mezi dvěma datovými soubory. 6668 Kromě toho kvartilní odchylka není ovlivněna extrémními hodnotami, kde obsahuje extrémní hodnoty. Koeficient odchylky kvartilu lze vypočítat tímto způsobem.

Koeficient kvartilní odchylky = (Q ₃ - Q ₁ ) / (Q ₃ + Q ₁ )

Koncept kvartilové odchylky a koeficientu kvartilu lze vysvětlit pomocí příkladu v určité sadě kroků.

Krok 1: Získejte sadu neseskupených dat

V prohlášení o problému jsme zvažovali běhy, které získal pálkař v posledních 20 testovacích zápasech: 96, 70, 100, 89, 78, 56, 45, 78, 68, 42, 66, 89, 90, 54, 44, 67, 87, 90, 97 a 98

Krok 2 : Seřadit data ve vzestupném pořadí:

42, 44, 45, 54, 56, 66, 67, 68, 70, 78, 78, 87, 89, 89, 90, 92, 96, 97, 98, 100

První kvartil ( Q ₁ )

Vypočítejte první kvartil

Q _i = i * (n + 1) / 4. pozorování

• Q ₁ = 1 * (20 + 1) / 4. pozorování
• Q ₁ = 5, 25. Pozorování

Takže 5, 25. Pozorování leží mezi pátou a šestou hodnotou v uspořádané skupině nebo uprostřed mezi 55 a 66

• Q ₁ = 55 + 0, 25 * (66 - 55)
• Q ₁ = 55 + 2, 75
• Q ₁ = 57, 25

Třetí kvartil (Q ₃ )

Výpočet třetího kvartilu je uveden jako:

Q _i = i * (n + 1) / 4. pozorování

• Q3 = i * (n + 1) / 4

• Q3 = 3 * (20 + 1) / 4. pozorování
• Q ₃ = 15, 75. Pozorování

Kde 15.75. leží mezi 15. a 16. hodnotou v objednané skupině

15. pozorování = 90

16. pozorování = 96

• Q3 = 90 +0, 75 * (96 - 90)
• Q3 = 90 + 4, 5
• Q3 = 94, 5

Krok 3 : Vypočítejte kvartilní odchylku a koeficient kvartilové odchylky na základě příslušného výsledku.

Kvartilní odchylka = (Q ₃ - Q ₁ ) / 2

• Kvartilní odchylka = (94, 5 - 57, 25) / 2
• Kvartilní odchylka = 18, 625

Koeficient kvartilní odchylky = (Q ₃ - Q ₁ ) / (Q ₃ + Q ₁ )

• Koeficient kvartilní odchylky = (94, 5 - 57, 25) / (94, 5 +57, 25)
• Koeficient kvartilní odchylky = 0, 2454

Relevance a použití vzorce kvartilové odchylky

• Kvartilní odchylka nebere v úvahu mnohem extrémnější body distribuce.
• QD se také mění s ohledem na změnu měřítka dat.
• Je to nejlepší měřítko pro otevřený systém.
• Méně ovlivněné kolísáním vzorků v datovém souboru
• Pouze závisí na centrálních hodnotách v distribuci.

Kalkulačka kvartilních odchylek

Můžete použít následující kalkulačku pro výpočet odchylky kvartilu

Q 3
Q 1
Kvartilní odchylka

Kvartilní odchylka

Q 3 - Q 1 = 2

0-0 = 0 2

Doporučené články

Toto je průvodce vzorcem Quartile Deviation Formula. Zde diskutujeme, jak vypočítat vzorec Quartile Deviation Formula spolu s praktickými příklady. Rovněž poskytujeme kalkulačku odchylek kvartil s šablonou Excel ke stažení. Další informace naleznete také v následujících článcích -

1. Příklad vzorce reálné úrokové sazby
2. Vzorec výnosů z prodeje
3. Vzorec pro podíl na trhu
4. Jak vypočítat čistý prodej?