
Aritmetický střední vzorec (obsah)
- Vzorec
- Příklady
- Kalkulačka
Co je aritmetický průměr?
Termín „aritmetický průměr“ se v zásadě týká matematického průměru dvou nebo více čísel. Metoda výpočtu aritmetického průměru se však může lišit v závislosti na frekvenci každé proměnné v souboru údajů - jednoduchý průměr (stejně vážený) nebo vážený průměr. Vzorec pro aritmetický průměr pro stejně vážené proměnné lze odvodit sečtením všech proměnných v datové sadě a pak vydělením výsledku počtem proměnných. Matematicky je reprezentován jako,
Arithmetic Mean = (x 1 + x 2 + …. + x n ) / n
nebo
Arithmetic Mean =∑ x i / n
Kde,
- x i = i th proměnná
- n = počet proměnných v datové sadě
V případě nerovnoměrně vážených proměnných lze vzorec pro aritmetický průměr odvodit součtem součinů každé proměnné a její frekvence a výsledek se pak vydělí součtem frekvencí. Matematicky je reprezentován jako,
Arithmetic Mean = (f 1 *x 1 +f 2 *x 2 + …. + f n *x n ) / (f 1 + f 2 + ….. + f n )
nebo
Arithmetic Mean = ∑ (f i * x i ) / f i
Kde
- x i = i th proměnná
- f i = Frekvence i- té proměnné
Příklady aritmetického průměrného vzorce (se šablonou Excel)
Vezměme si příklad, abychom lépe pochopili výpočet aritmetického průměru.
Tuto šablonu aritmetických průměrných vzorců Excel si můžete stáhnout zde - šablony aritmetických průměrných vzorců ExcelAritmetický střední vzorec - příklad č. 1
Vezměme si příklad batsmana, který během posledního roku zaznamenal následující běhy v posledních 10 směnách: 45, 65, 7, 10, 43, 35, 25, 17, 78, 91. Vypočítejte si průměr batsmana v jeho posledním 10 směn.
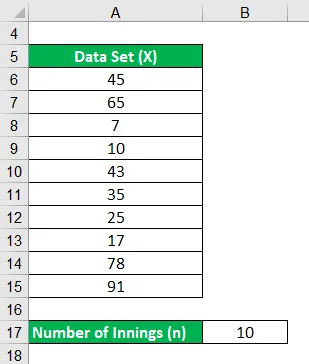
Řešení:
Aritmetický průměr se počítá pomocí vzorce uvedeného níže
Aritmetický průměr = ∑ x i / n
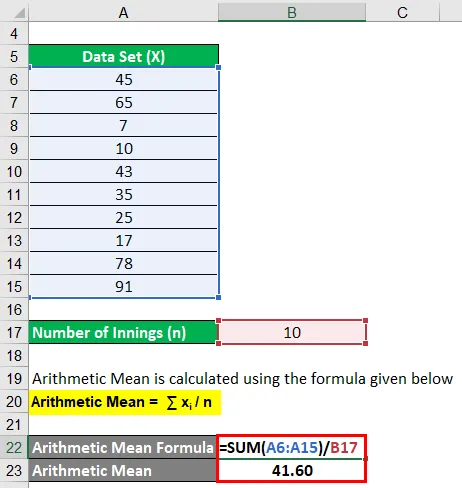
- Aritmetický průměr = (45 + 65 + 7 + 10 + 43 + 35 + 25 + 17 + 78 + 91) / 10
- Aritmetický průměr = 41, 60
Průměr batsmana tedy zůstal 41, 60 běhů za směny v jeho posledních 10 směnách.
Aritmetický střední vzorec - Příklad č. 2
Vezměme si příklad třídy se 45 studenty. V poslední době proběhl týdenní test pro vědu, ve kterém byli studenti hodnoceni na stupnici od 1 do 10. Na základě následujících informací vypočítejte průměrné známky v testu.
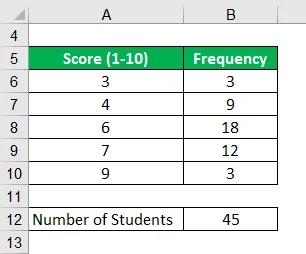
Řešení:
Aritmetický průměr se počítá pomocí vzorce uvedeného níže
Aritmetický průměr = ∑ (f i * x i ) / f i
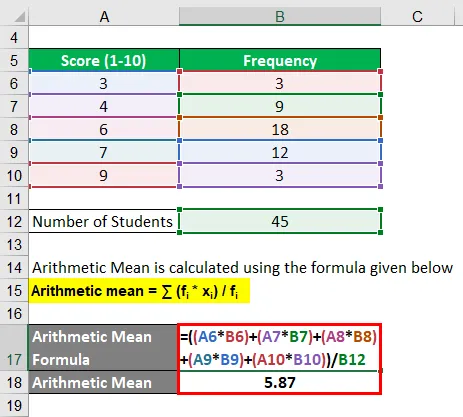
- Aritmetický průměr = ((3 * 3) + (4 * 9) + (6 * 18) + (7 * 12) + (9 * 3)) / 45
- Aritmetický průměr = 264/45
- Aritmetický průměr = 5, 87
Průměrné skóre ve vědecké zkoušce tedy bylo 5, 87.
Aritmetický střední vzorec - Příklad č. 3
Vezměme si příklad dvou sad dat se dvěma různými aritmetickými prostředky. První sada dat má 10 proměnných s průměrem 45, zatímco druhá sada dat má 7 proměnných a průměr 42. Určete aritmetický průměr z obou souborů dat dohromady.
Řešení:
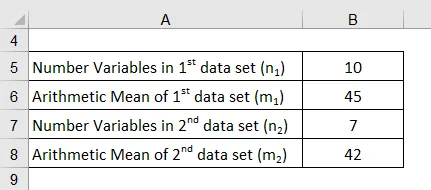
Aritmetické prostředky kombinovaného souboru dat se vypočítají pomocí vzorce uvedeného níže
Aritmetický průměr = ((m 1 * n 1 ) + (m 2 * n 2 )) / (n 1 + n 2 )
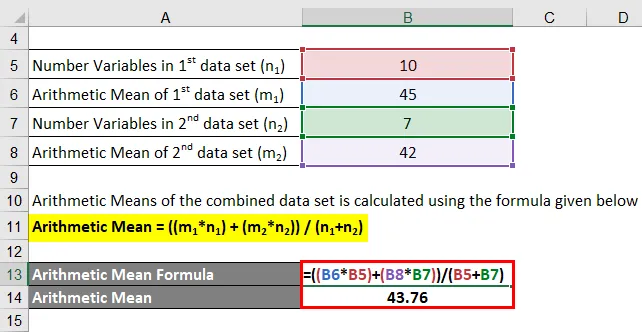
- Aritmetický průměr = (45 * 10 + 42 * 7) / (10 + 7)
- Aritmetický průměr = 43, 76
Aritmetický průměr kombinovaného souboru dat je proto 43, 76.
Vysvětlení
Vzorec pro aritmetický průměr lze vypočítat pomocí následujících kroků:
Krok 1: Nejprve shromážděte a seřiďte proměnné, pro které je třeba vypočítat aritmetický průměr. Proměnné jsou označeny x i .
Krok 2: Dále určete počet proměnných v datové sadě a v případě stejně vážených proměnných je označeno n. Jinak určete frekvenci každé proměnné a jsou označeny f i a počet proměnných je součtem frekvencí.
Krok 3: Konečně lze vzorec pro aritmetický průměr pro stejně vážené proměnné odvodit přidáním všech proměnných a výsledek se pak vydělí počtem proměnných v sadě dat, jak je uvedeno níže.
Aritmetický průměr = ∑ x i / n
V případě váženého průměru však lze vzorec pro aritmetický průměr odvodit součtem součinů každé proměnné a její frekvence a výsledek se pak vydělí součtem frekvencí, jak je uvedeno níže.
Aritmetický průměr = ∑ f i * x i / f i
Relevance a použití aritmetického průměrného vzorce
Koncept aritmetického průměru je velmi jednoduchý a elementární. Je to však stále velmi důležité, protože se často používá jako statistický ukazatel k hodnocení průměrného výsledku v souboru údajů. Ve skutečnosti umožňuje vyhodnotit, které z proměnných jsou lepší nebo nižší než průměr skupiny. Používá se také jako měřítko k vyjádření průměrné hodnoty v celé datové řadě. Aritmetický průměr se dále používá v případech, kdy geometrický průměr nebo harmonické prostředky jsou méně užitečné, jako je průměrná známka, hmotnost atd.
Aritmetický průměrný vzorec kalkulačka
Můžete použít následující aritmetickou střední kalkulačku
| x 1 | |
| x 2 | |
| x 3 | |
| x 4 | |
| n | |
| Aritmetický průměr | |
| Aritmetický průměr | = |
|
|
Doporučené články
Toto je průvodce aritmetickým průměrem vzorce. Zde diskutujeme, jak vypočítat aritmetický průměr spolu s praktickými příklady. Poskytujeme také aritmetický průměrný kalkulačka se stahovatelnou šablonou Excel. Další informace naleznete také v následujících článcích -
- Jak vypočítat harmonický průměr?
- Průvodce po formulaci průměrné populace
- Výpočet střední hodnoty pomocí vzorce
- Příklady vzorce čistého prodeje