
Úvod do série Fibonacci v Pythonu
Fibonacciho řada v Pythonu se označuje jako řada čísel, kde další číslo je součet současných dvou čísel.
Například:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 .. dále
Takže zde 0 + 1 = 1
1 + 1 = 2
1 + 2 = 3
2 + 3 = 5
3 + 5 = 8
5 + 8 = 13
8+ 13 = 21 atd.
Při pohledu na výše uvedené by člověk získal určitou představu o tom, o čem mluvíme.
Z hlediska matematického pravidla však lze psát jako:

Kde n-té číslo je součet čísla na místech (n-1) a (n-2). Pokud jde o implementaci série Fibonacci, mohlo by existovat množství kódovacích jazyků, prostřednictvím kterých by se to dalo dělat.
V dnešní době je však Python široce používaným jazykem. Podívejme se na implementaci série Fibonacci prostřednictvím Pythonu. Dříve než budete pokračovat, měli byste si být vědomi základních příkazů o kondici, jako je smyčka, if-else, while loop atd. V Pythonu. Pokud ne, bylo by skvělé, kdyby se to dalo revidovat a pak převzít nadcházející obsah. Zde pro demonstrační účely používám spyder, který je IDE pro programovací jazyk python. K provádění programů Python lze použít i jiné notebooky IDE nebo Ipython.
Fibonacciho série v Pythonu
Podívejme se na implementaci Fibonacciho čísla a řady s ohledem na 1. dva prvky Fibonacci jsou 0 a 1:
Funkci Fibonacci však můžete vyladit podle svého požadavku, ale nejprve si prohlédněte základní informace a postupně přejděte k ostatním.
Pythonův kód pro nalezení n-tého Fibonacciho čísla
Kód 1:
def Fibonacci_num(m):
u = 0
v = 1
if m < 0:
print("Incorrect input entered")
elif m == 0:
return u
elif m == 1:
return v
else:
for i in range(2, m):
c = u + v
u = v
v = c
return v
Kód 2:
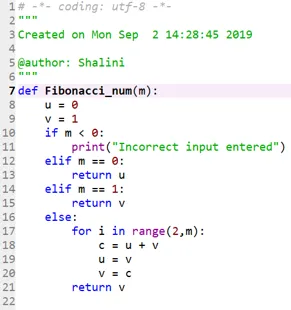
Výstup:
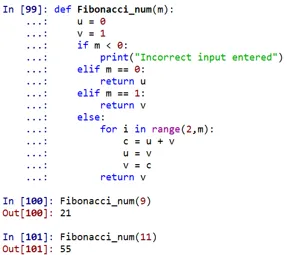
Jak je vidět, Fibonacciho číslo na 9. místě bude 21 a na 11. místě 55.
- Zde je „fibonacci_num“ definována funkce, která se za určitých podmínek stará o nalezení Fibonacciho čísla. Tuto funkci lze vyvolat zadáním libovolné polohy.
Nyní se podívejme, jak je možné tisknout řady do uvedené pozice:
Kód:
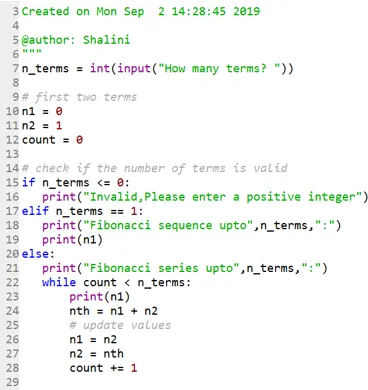
Výstup:
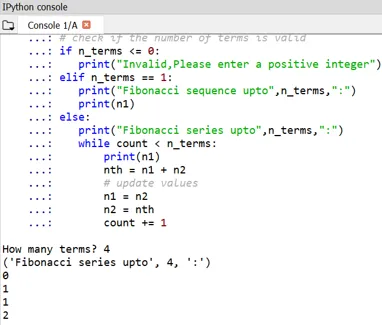
Lze si všimnout, že začátek Fibonacciho čísla je definován jako 0 a 1.
- Pokud chce někdo definovat své vlastní počáteční termíny, může to být provedeno stejným způsobem vyladěním n1 a n2. Zde je příklad toho:
Řekněme, že nyní chceme, aby naše počáteční termíny byly: n1 = 3, n2 = 5
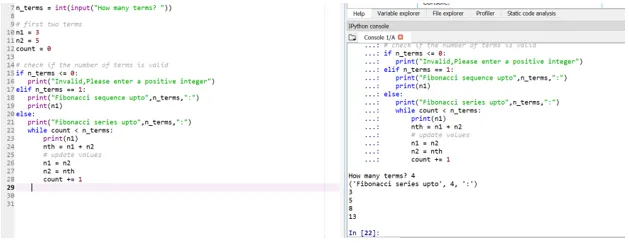
Zde se vaše 4. funkční období (vstup uživatele zaujme) rozhodne na základě vašich počátečních podmínek.
Metody, kterými lze generovat řadu Fibonacci
Níže jsou uvedeny tři metody, pomocí nichž lze generovat řadu Fibonacci:
1. Prostřednictvím generátorů
Kód:
def fibo(num):
a, b = 0, 1
for i in xrange(0, num):
yield "():: ()".format(i + 1, a)
a, b = b, a + b
for item in fibo(10):
print item
Výstup:
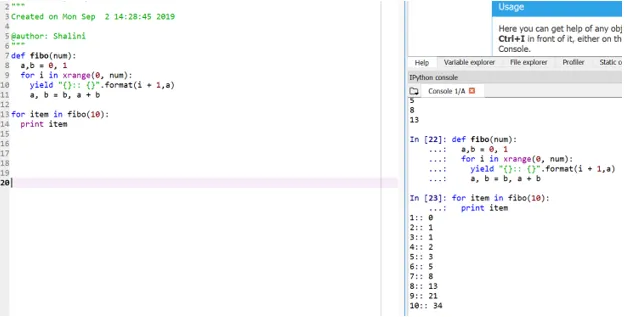
Tato metoda se označuje jako „generátor“, protože funkce xrange je generátor čísel mezi 0 a num a výnos je generátor pro formátovaný výstup.
Tady je to, co pro vás xrange dělá:

Zde byla série Fibonacci definována ve formě funkce, ve které se funkce smyčky, funkce xrange a výnos stará o výstup.
2. Pro smyčku
Kód:
u, v = 0, 1
for i in xrange(0, 10):
print u
u, v = v, u + v
Výstup:

Jak je vidět, byl použit jednoduchý cyklus pro tisk řady Fibonacci mezi 0 a 10. Uvnitř smyčky byly proměnným přiřazeny nové hodnoty. U a v jsou výchozí počáteční hodnoty Fibonacci, které byly nastaveny na 0, respektive 1.
Pokud jde o postupování smyčky, nová hodnota u je stará hodnota v, zatímco nová hodnota v je součtem starých hodnot u a v. To pokračuje až do konce hodnot rozsahu.
3. Prostřednictvím rekurze
Kód:
#Through recursion
def fibonacci_ser(m):
if(m <= 1):
return m
else:
return(fibonacci_ser(m-1) + fibonacci_ser(m-2))
m = int(input("Enter number of terms:"))
print("Fibonacci sequence:")
for i in range(m):
print fibonacci_ser(i),
Výstup:
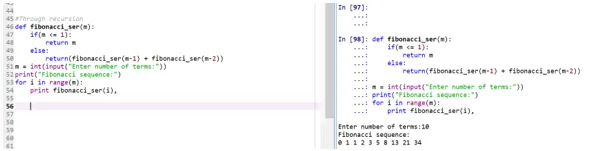
- Funkce „fibonacci_ser“ je výzvou k vytištění řady Fibonacci.
- Metoda tedy získala název „rekurze“.
Následovaly kroky:
- Zde byl uživatel vyzván k zadání místa, do kterého musí být série Fibonacci vytištěny.
- Číslo prochází funkcí „fibonacci_ser“.
- Podmínka je zkontrolována, pokud je poskytovaná délka menší než 1 nebo není. Pokud ano, výsledek je uveden okamžitě.
- Pokud je však délka větší než 1, provede se rekurzivní volání na „fibonacci_ser“ s argumenty, které mají délku menší než 1 a 2, tj. Fibonacci_ser (m-1) a fibonacci_ser (m-2).
- Rekurze tedy poskytuje požadovaný výstup a tiskne ji.
- Stručně řečeno, diskutovali jsme o třech způsobech zobrazení řady Fibonacci.
- Pro smyčku, generátory a rekurzi.
Shrnutí všech tří Pythonových kódů
Níže jsou tři pythonové kódy:
1. Prostřednictvím generátorů
Kód:
def fibo(num):
a, b = 0, 1
for i in xrange(0, num):
yield "():: ()".format(i + 1, a)
a, b = b, a + b
for item in fibo(10):
print item
2. Pro smyčku
Kód:
u, v = 0, 1
for i in xrange(0, 10):
print u
u, v = v, u + v
3. Prostřednictvím rekurze
Kód:
def fibonacci_ser(n):
if(n <= 1):
return n
else:
return(fibonacci_ser(n-1) + fibonacci_ser(n-2))
n = int(input("Enter number of terms:"))
print("Fibonacci sequence:")
for i in range(n):
print fibonacci_ser(i),
Shrneme-li výše, jsou všechny postupy, je třeba praktikovat, abychom se dobře uchopili.
Výstup:
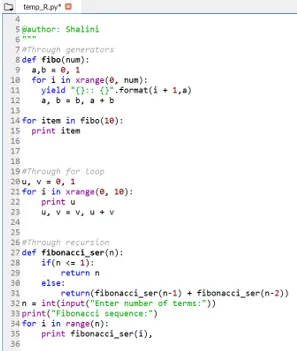
Závěr
Při procházení výše uvedeným obsahem Fibonacci by člověk měl křišťálově jasné porozumění Fibonacciho číslům a sériím specializovaným na python. Jakmile si člověk osvojí logiku série Fibonacci, vygeneruje další sadu řad, bude pracovat s jinými čísly a různými metodami. Jediným způsobem, jak v tom vyniknout, je logický přístup.
Doporučené články
Toto je průvodce po sérii Fibonacci v Pythonu. Zde diskutujeme Fibonacciho čísla a řady specializované na python, vytváříme další sadu řad, pracujeme s jinými čísly a různými metodami. Další informace naleznete také v dalších souvisejících článcích -
- Generátor náhodných čísel v Pythonu
- Matematické funkce v Pythonu
- Factorial v Pythonu
- Zapouzdření v Pythonu
- Fibonacciho řada v Javě
- Funkce Pythonu
- Věcný program v JavaScriptu
- Generátor náhodných čísel v Matlabu
- Generátor náhodných čísel v C #
- Zapouzdření do JavaScriptu