Úvod do Heap Sort in C
Třídění je technika, která se týká řazení prvků na základě různých vlastností. (Vlastnosti jako uspořádání dat ve vzestupném, sestupném nebo abecedním pořadí). Jedním z hlavních příkladů třídění, na které zde můžeme myslet, je řazení položek během online nakupování. Můžeme se týkat cen, popularity, nejnovějších a tak dále. Existuje tedy mnoho technik pro toto umísťování prvků pomocí třídění. V tomto tématu se dozvíme o Heap Sort in C.
Zde se naučíme jednu z nejčastějších třídicích technik, Heap Sort, prostřednictvím programovacího jazyka C.
Logika pro řazení haldy
Jak vlastně můžeme provést třídění haldy? Pojďme se podívat níže.
Za prvé, halda je jednou ze stromových datových struktur. Strom zde zapojený je vždy kompletní binární strom. A existují dva druhy haldy
- Min - Heap: Obecně uspořádáno ve vzestupném pořadí, to znamená, pokud prvek nadřazeného uzlu má hodnotu menší než hodnota podřízených prvků uzlu.
- Max - Heap: Obecně uspořádáno v sestupném pořadí, to znamená, pokud prvek nadřazeného uzlu má hodnotu vyšší než hodnota prvků podřízeného uzlu.
Kroky pro řazení haldy
- Jakmile jsou získána netříděná data seznamu, jsou prvky uspořádány ve struktuře dat haldy buď na základě vytvoření hromady min nebo haldy haldy.
- První prvek z výše uvedeného seznamu je přidán do našeho pole
- Opět se vytvoří technika datové struktury hlavy, která je stejná jako v prvním kroku, a opět je vybrán a přidán do našeho pole buď nejvyšší prvek, nebo nejmenší prvek.
- Opakované kroky nám pomáhají získat pole se seřazeným seznamem.
Program pro řazení haldy v C
#include
int main()
(
int h(20), num, i, j, root, t, x;
printf("Enter number of elements :");
scanf("%d", &num);
printf("\nEnter the elements : ");
for (i = 0; i < num; i++)
scanf("%d", &h(i));
// build max heap
for(i=0;i (
x=i;
do
(
root = (x - 1) / 2;
if (h(root) < h(x))
(
t = h(root);
h(root) = h(x);
h(x) = t;
)
x = root;
) while (x != 0);
)
printf("Heap array formed is: ");
for (i = 0; i < num; i++)
printf("%d\t ", h(i));
for (j = num - 1; j >= 0; j--)
(
t = h(0);
h(0) = h(j);
h(j) = t;
root = 0;
do
(
x = 2 * root + 1;
if ((h(x) < h(x + 1)) && x < j-1)
x++;
if (h(root) (
t = h(root);
h(root) = h(x);
h(x) = t;
)
root = x;
) while (x < j);
)
printf("\nThe sorted array is : ");
for (i = 0; i < num; i++)
printf("\t %d", h(i));
)#include
int main()
(
int h(20), num, i, j, root, t, x;
printf("Enter number of elements :");
scanf("%d", &num);
printf("\nEnter the elements : ");
for (i = 0; i < num; i++)
scanf("%d", &h(i));
// build max heap
for(i=0;i (
x=i;
do
(
root = (x - 1) / 2;
if (h(root) < h(x))
(
t = h(root);
h(root) = h(x);
h(x) = t;
)
x = root;
) while (x != 0);
)
printf("Heap array formed is: ");
for (i = 0; i < num; i++)
printf("%d\t ", h(i));
for (j = num - 1; j >= 0; j--)
(
t = h(0);
h(0) = h(j);
h(j) = t;
root = 0;
do
(
x = 2 * root + 1;
if ((h(x) < h(x + 1)) && x < j-1)
x++;
if (h(root) (
t = h(root);
h(root) = h(x);
h(x) = t;
)
root = x;
) while (x < j);
)
printf("\nThe sorted array is : ");
for (i = 0; i < num; i++)
printf("\t %d", h(i));
)#include
int main()
(
int h(20), num, i, j, root, t, x;
printf("Enter number of elements :");
scanf("%d", &num);
printf("\nEnter the elements : ");
for (i = 0; i < num; i++)
scanf("%d", &h(i));
// build max heap
for(i=0;i (
x=i;
do
(
root = (x - 1) / 2;
if (h(root) < h(x))
(
t = h(root);
h(root) = h(x);
h(x) = t;
)
x = root;
) while (x != 0);
)
printf("Heap array formed is: ");
for (i = 0; i < num; i++)
printf("%d\t ", h(i));
for (j = num - 1; j >= 0; j--)
(
t = h(0);
h(0) = h(j);
h(j) = t;
root = 0;
do
(
x = 2 * root + 1;
if ((h(x) < h(x + 1)) && x < j-1)
x++;
if (h(root) (
t = h(root);
h(root) = h(x);
h(x) = t;
)
root = x;
) while (x < j);
)
printf("\nThe sorted array is : ");
for (i = 0; i < num; i++)
printf("\t %d", h(i));
)
Nejprve žádáme uživatele, aby vložil počet prvků, které jsou vzaty pro třídění, a pak uživatel může zadat různé prvky, které mají být seřazeny.
Následovaly kroky
- Dalším zaměřením je vytvoření pole haldy, v tomto případě pole max-haldy.
- Hlavní podmínkou pro získání matice max - haldy je ověření, že žádná hodnota nadřazeného uzlu není nižší než hodnota podřízeného uzlu. Budeme vyměňovat, dokud nedosáhneme této podmínky.
- Hlavní výhoda v tomto úplném binárním stromu je, že k levým a pravým podřízeným uzlům nadřazeného uzlu lze přistupovat s hodnotami 2 (i) + 1 a 2 * (i) + 2. Kde i je nadřazený uzel.
- Tímto způsobem zde umístíme náš kořenový uzel, který obsahuje maximální hodnotu, na nejvzdálenější uzel listu. A pak opět stejným postupem tak, že další maximální počet se nyní stane kořenovým uzlem.
- Budeme postupovat stejným způsobem, dokud v poli haldy nezůstane pouze jeden uzel.
- A pak uspořádáme naše haldy do podoby dokonalého seřazeného pole ve vzestupném pořadí.
- Nakonec vytiskneme seřazené pole ve výstupu.
Výstup:
Výstup je připojen níže.
Ukážu vám obrazové znázornění událostí:
- Zadaná data jsou nejprve představována ve formě jednorozměrného pole následujícím způsobem.

- Obrazová reprezentace vytvořeného binárního stromu je následující:
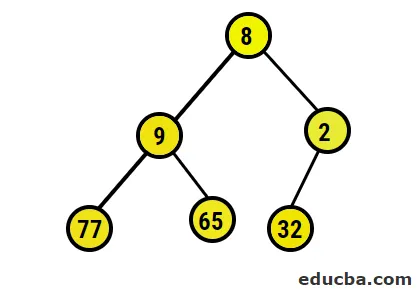
- Nyní se chystáme převést na maximální hromadu tím, že se ujistíme, že všechny nadřazené uzly jsou vždy větší než podřízené uzly. Jak je uvedeno ve výstupu pod polem seřazeným do haldy, obrazová reprezentace bude:
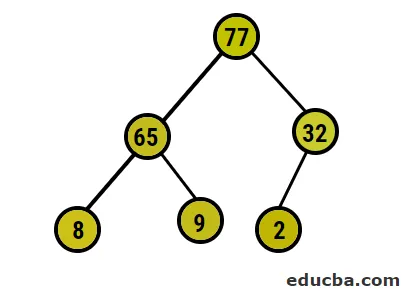
- Poté zaměníme kořenový uzel za extrémní listový uzel a poté jej ze stromu odstraníme. Uzel listu bude nyní kořenem a znovu stejný proces e, který opět získá nejvyšší prvek v kořenovém adresáři
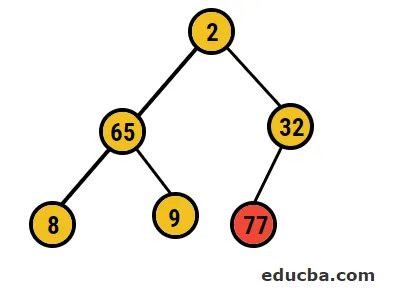
- V tomto případě se z tohoto stromu odstraní 77 číslic a umístí se do našeho tříděného pole a proces se opakuje.
Výše jsme to viděli pro vytváření max haldy pole. Tentýž proces se zabývá také sestavením matice min. Haldy. Jak bylo uvedeno výše, jediný rozdíl je ve vztahu mezi elementy nadřazený a podřízený uzel.
Jako cvičení můžete zkusit utřídit haldy v sestupném pořadí?
Závěr
Přestože existuje mnoho třídicích technik, je řazení haldy považováno za jednu z lepších třídicích technik kvůli své časové a prostorové složitosti. Časová složitost pro všechny nejlepší, průměrné a nejhorší případy je O (nlogn), kde nejhorší případová složitost je lepší než nejhorší případová složka Quicksort a prostorová složitost je O (1).
Doporučené články
Toto je průvodce uspořádáním haldy v C. Zde diskutujeme logiku a kroky pro řazení haldy s ukázkovým kódem a výstupem spolu s obrázkovými znázorněními. Další informace naleznete také v následujících článcích -
- Hromadné řazení v Javě
- Výběr Seřadit v Javě
- Palindrom v programu C
- Vzory v programování C
- Hromadné řazení v C ++ (algoritmus)
- Haldy Seřadit v Pythonu
- C Programovací násobení matic