Úvod do hierarchického klastru
- Nedávno jeden z našich klientů požádal náš tým, aby vydal seznam segmentů s pořadí důležitosti v rámci svých zákazníků, aby je zacílili na franšízu jednoho ze svých nově zavedených produktů. Je zřejmé, že pouhým segmentováním zákazníků pomocí částečného klastrování (k-znamená, c-fuzzy) se neprojeví pořadí důležitosti, na které přichází hierarchické klastrování.
- Hierarchické shlukování rozděluje data do různých skupin na základě některých opatření podobnosti známých jako klastry, které se v zásadě zaměřují na budování hierarchie mezi klastry. Je to v podstatě bez dozoru učení a výběr atributů pro měření podobnosti je specifický pro konkrétní aplikaci.
Shluk datové hierarchie
- Aglomerační klastrování
- Divisive Clustering
Vezměme si příklad dat, známek získaných 5 studenty, které je seskupí pro nadcházející soutěž.
| Student | Známky |
| A | 10 |
| B | 7 |
| C | 28 |
| D | 20 |
| E | 35s |
1. Aglomerační shlukování
- Začneme tím, že každý jednotlivý bod / prvek zde považujeme za klastry a pokračujeme ve slučování podobných bodů / prvků do nového klastru na nové úrovni, dokud nám nezůstane jediný klastr, což je přístup zdola nahoru.
- Jedním spojením a úplným spojením jsou dva populární příklady aglomeračního shlukování. Jiné než průměrné a středové spojení. V jednom spojení spojíme v každém kroku dva klastry, jejichž dva nejbližší členové mají nejmenší vzdálenost. V úplném propojení se spojíme s členy nejmenší vzdálenosti, které poskytují nejmenší maximální párovou vzdálenost.
- Proximitní matice, je to jádro pro provádění hierarchického shlukování, které dává vzdálenost mezi jednotlivými body.
- Vytvořme si proximitní matici pro naše data uvedená v tabulce, protože vypočítáváme vzdálenost mezi jednotlivými body s ostatními body, bude to asymetrická matice tvaru n × n, v našem případě 5 × 5 matic.
Populární metoda pro výpočet vzdálenosti je:
- Euklidovská vzdálenost (na druhou)
dist((x, y), (a, b)) = √(x - a)² + (y - b)²
- Manhattanská vzdálenost
dist((x, y), (a, b)) =|x−c|+|y−d|
Euklidovská vzdálenost se nejčastěji používá, budeme ji používat stejně a půjdeme se složitým propojením.
| Student (klastry) | A | B | C | D | E |
| A | 0 | 3 | 18 | 10 | 25 |
| B | 3 | 0 | 21 | 13 | 28 |
| C | 18 | 21 | 0 | 8 | 7 |
| D | 10 | 13 | 8 | 0 | 15 |
| E | 25 | 28 | 7 | 15 | 0 |
Diagonální prvky proximitní matice budou vždy 0, protože vzdálenost mezi bodem se stejným bodem bude vždy 0, proto jsou diagonální prvky vyňaty z úvahy pro seskupování.
Zde v iteraci 1 je nejmenší vzdálenost 3, proto sloučíme A a B a vytvoříme shluk, znovu vytvoříme novou proximitní matici s shlukem (A, B) a vezmeme (A, B) shlukový bod jako 10, tj. Maximum ( 7, 10) tak by nově vytvořená proximitní matice byla
| Clustery | (A, B) | C | D | E |
| (A, B) | 0 | 18 | 10 | 25 |
| C | 18 | 0 | 8 | 7 |
| D | 10 | 8 | 0 | 15 |
| E | 25 | 7 | 15 | 0 |
V iteraci 2, 7 je minimální vzdálenost, proto sloučíme C a E a vytvoříme nový klastr (C, E), opakujeme proces následovaný v iteraci 1, dokud neskončíme s jediným klastrem, tady zastavíme v iteraci 4.
Celý proces je znázorněn na následujícím obrázku:
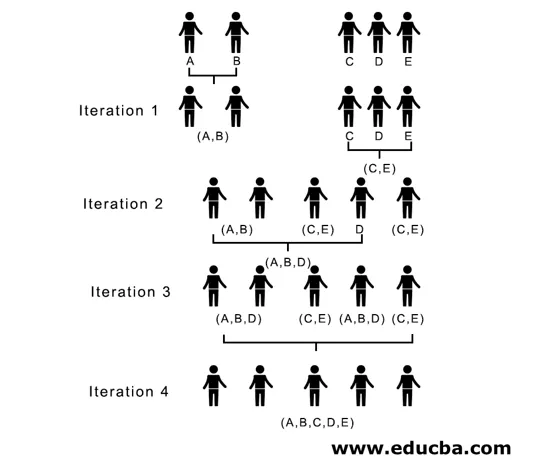
(A, B, D) a (D, E) jsou 2 klastry vytvořené při iteraci 3, při poslední iteraci vidíme, že nám zbývá jediný klastr.
2. Divisive Clustering
Začneme tím, že budeme považovat všechny body za jeden klastr a oddělíme je nejvzdálenější vzdáleností, dokud neskončíme jednotlivými body jako jednotlivé klastry (ne nutně se můžeme zastavit uprostřed, záleží na minimálním počtu prvků, které chceme v každém klastru) v každém kroku. Je to právě opak aglomeračního klastru a jedná se o přístup shora dolů. Dělící klastrování je způsob, jak se opakující k znamená klastrování.
Volba mezi aglomeračním a dělitelným klastrem je opět závislá na aplikaci, přesto je třeba zvážit několik bodů:
- Divisive je složitější než aglomerativní shlukování.
- Rozdělovací klastrování je efektivnější, pokud negenerujeme úplnou hierarchii až po jednotlivé datové body.
- Aglomerační klastrování se rozhoduje na základě zvážení místních patterů, aniž by zpočátku zohledňovaly globální vzorce, které nelze zvrátit.
Vizualizace hierarchického klastru
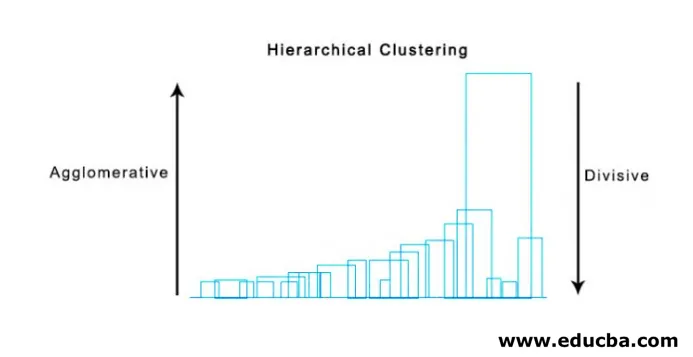
Velmi užitečnou metodou vizualizace hierarchického shlukování, která pomáhá v podnikání, je Dendogram. Dendogramy jsou stromové struktury, které zaznamenávají posloupnost sloučení a rozdělení, ve kterých svislá čára představuje vzdálenost mezi shluky, vzdálenost mezi svislými čarami a vzdálenost mezi shluky je přímo úměrná, tj. Čím větší je pravděpodobnost, že shluky budou rozdílné, bude tím větší.
Můžeme použít dendogram k rozhodnutí o počtu shluků, stačí nakreslit čáru, která se protíná s nejdelší svislou čarou na dendogramu, počet svislých čar protínaných bude počet shluků, které mají být zváženy.
Níže je uveden příklad Dendogram.
Existují velmi jednoduché a přímé pythonové balíčky a jeho funkce pro provádění hierarchického shlukování a vykreslování dendogramů.
- Hierarchie ze scipy.
- Cluster.hierarchy.dendogram pro vizualizaci.
Běžné scénáře, ve kterých se používá hierarchické shlukování
- Segmentace zákazníků na marketing produktů nebo služeb.
- Územní plánování k identifikaci míst pro stavbu struktur / služeb / budovy.
- Analýza sociálních sítí, například, identifikujte všechny fanoušky MS Dhoni, aby propagovali jeho biopic.
Výhody hierarchického klastru
Výhody jsou uvedeny níže:
- V případě částečného klastrování jako k-znamená, počet klastrů by měl být znám před klastrováním, což není možné v praktických aplikacích, zatímco v hierarchickém klastrování není vyžadována předchozí znalost počtu klastrů.
- Hierarchické shlukování vytváří hierarchii, tj. Strukturu více informativní než nestrukturovaná sada plochých shluků vrácená částečným shlukováním.
- Hierarchické klastrování lze snadno implementovat.
- Ve většině scénářů přináší výsledky.
Závěr
Typ shlukování dělá velký rozdíl při prezentaci dat, hierarchické shlukování více informativní a snadno analyzovatelné je výhodnější než částečné shlukování. A to je často spojeno s tepelnými mapami. Nezapomenout na atributy zvolené pro výpočet podobnosti nebo odlišnosti převážně ovlivňuje klastry i hierarchii.
Doporučené články
Toto je průvodce hierarchickým klastrem. Zde diskutujeme úvod, výhody hierarchického klastru a běžné scénáře, ve kterých se hierarchické klastry používají. Další informace naleznete také v dalších navrhovaných článcích -
- Clustering Algorithm
- Shlukování ve strojovém učení
- Hierarchické shlukování v R
- Metody shlukování
- Jak odstranit hierarchii v Tableau?