
Úvod do slučovacího třídění v JavaScriptu
Algoritmy třídění jsou v informatice velmi důležité. Výstupem třídění je uspořádat prvky seznamu do určitého pořadí (buď vzestupně nebo sestupně). Sloučit třídění v JavaScriptu je jeden z nejúčinnějších dostupných algoritmů třídění, protože je založen na konceptu dělení a dobývání. Jak název napovídá, nejprve rozdělte větší problém na malé problémy, než vyřešte menší problémy, abyste vyřešili větší problém. Koncepčně je sloučení třídění kombinací dvou základních algoritmů nazývaných MERGE a MERGE_SORT.
který funguje takto:
- Rozdělte netříděný seznam na n počet dílčích seznamů jednotlivých položek (n je celkový počet prvků v netříděném seznamu).
- Opakovaně slučujte seznamy do tříděných seznamů, dokud nebude k dispozici pouze jeden seznam.
Implementace slučovacího třídění v JavaScriptu
Algoritmus MERGE sleduje postup kombinování dvou tříděných seznamů do jednoho tříděného seznamu.
Příklad: Předpokládejme, že existují dva seznamy, tj. Seznam 1 (1, 5, 3) a Seznam 2 (7, 2, 9).
1. Nejprve seřaďte oba seznamy.
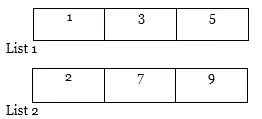
Nyní na to uvidíme a použijeme techniku E.
2. Poté vytvoříme nový seznam velikostí x + y, kde x je počet prvků v seznamu 1 a y je počet prvků v seznamu 2.

V našem případě x = 3 a y = 3, takže x + y = 6.
3. Nyní máme dva ukazatele.
První ukazatel směřující na první pozici seznamu 1 a druhý ukazatel směřující na první pozici seznamu 2.

4. Potom porovnáme hodnotu obou ukazatelů. Ukazatel s menší hodnotou, zkopírujte tento prvek do Seznamu 3 a přesuňte ukazatel napravo od seznamu s menší hodnotou a výsledným seznamem (tj. Seznam 1 a Seznam 3)

5. Podobně proveďte krok 4 znovu a znovu.

Další traverz… ..
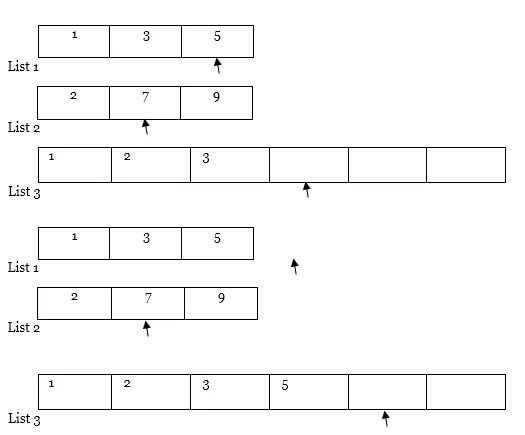
Poznámka : Pokud jeden ze seznamů (tj. Seznam 1 nebo seznam 2) zcela projde jako v případě, zkopírujte celý obsah jiného seznamu ze ukazatele do seznamu výsledků (tj. Seznam 3) následujícím způsobem.

Pseudo kód
Function merge (sublist1, sublist2) (
Create var for result list
While sublist1 length > 0 and sublist2 length > 0
If sublist1(0) < sublist2(0) Copy the sublist1 pointer value to result list and Shift pointer of sublist1 to right
else
Copy the sublist2 pointer value to result list and Shift pointer of sublist2 to right
Return concat sublist1 or sublist2 (depending if node1 is empty or not)
Algoritmus MERGE_SORT rozdělí daný netříděný seznam na minimální velikost a poté volá algoritmus MERGE, aby tento seznam zkombinoval do nového tříděného seznamu.
Pseudo kód
function mergeSort(list) (
If list length < 2
Return list
Create var for middle index of list
Create var for left index of list
Create var for right index of list
Recursively call mergeSort function
)
Příklad
Zde sledujeme implementaci sloučení řazení shora dolů. Začíná nahoře a pokračuje směrem dolů, s každým rekurzivním tahem a položením stejné otázky „Co je třeba udělat pro seřazení seznamu?“ A po odpovědi je „Rozdělit seznam na dva, uskutečnit rekurzivní volání a sloučit Výsledek".
Kód v Javascriptu
// Split the list into halves and merge them recursively
function mergeSort (list) (
if (list.length < 2) (
return list;// return once we hit a list with a single element
)
var mid = Math.floor(list.length / 2);
var left = mergeSort(list.slice(0, mid));
var right = mergeSort(list.slice(mid));
return merge(left, right);
)
// compare the lists element by element and return the concatenated resultList
function merge (sublist1, sublist2) (
var resultList = ();
while (sublist1.length > 0 && sublist2.length > 0)
resultList.push(sublist1(0) < sublist2(0)? sublist1.shift() : sublist2.shift());
return resultList.concat(sublist1.length? sublist1 : sublist2);
)
const list = (6, 5, 3, 1, 8, 7, 2, 4, 2, 5, 1, 2, 3) console.log(mergeSort(list)) //( 1, 1, 2, 2, 2, 3, 3, 4, 5, 5, 6, 7, 8 )
Hlavní funkce slučovacího řazení rozdělí daný seznam do menších seznamů v každé iteraci rekurzivního volání. Nezapomeňte, že rekurze vyžaduje základní podmínku, aby se zabránilo nekonečné rekurzi. V našem případě máme:
if (list.length < 2) (
return list;// return once we hit a list with a single element
)
Poté, co nastavíme základní podmínku pro rekurzi, identifikujeme prostřední index, který daný seznam rozdělí na levý a pravý dílčí seznam, jak je vidět výše na příkladu. Pak musíme sloučit levý podadresář a pravý podadresář, který nyní uvidíme. Ve výše uvedené funkci sloučení musíme zajistit, že třídíme všechny prvky v levém podadresáři a pravém podadresáři. seznam. Způsob, jakým to uděláme, je pomocí smyčky while. Ve smyčce while porovnáme jeden po druhém prvek v levém pod-seznamu a prvek v pravém pod-seznamu. Můžeme zatlačit menší z těchto dvou do seznamu výsledků a podle toho přesunout kurzor levého a dolního seznamu. Nakonec musíme zřetězit seznam výsledků. Toto je velmi důležité! Pokud zde neuděláme tento poslední krok, budeme mít na konci neúplný seznam prvků, protože podmínka smyčky while selže, jakmile jeden ze dvou ukazatelů dosáhne konce.
Výstup:

Vlastnosti sloučení třídění
- Sloučit řazení je stabilní, protože stejný prvek v poli udržuje své původní polohy vůči sobě navzájem.
- Sloučit řazení není „na místě“, protože při slučování vytvoří kopii celého seznamu. Z tohoto důvodu je složitost prostoru (O (n)) tohoto algoritmu ve skutečnosti větší než u ostatních a neměla by být použita ve složitých problémech, kde je prostor nadstandardní.
- Celková časová složitost sloučení je O (nLogn). Je efektivnější, protože v nejhorším případě je také runtime O (nlogn).
Závěr
Sloučit řazení nejlepší, nejhorší a průměrná doba složitosti času jsou stejné, což z něj činí efektivnější algoritmus. Funguje to rychleji než jiné techniky třídění. Sloučit řazení lze použít na soubory libovolné velikosti. Je vysoce paralelizovatelný díky použití metody dělení a dobytí. Chcete-li vyvinout silné základy v oblasti informatiky, doporučujeme vám důkladně porozumět různým třídicím algoritmům.
Doporučený článek
Toto byl průvodce sloučením třídění v JavaScriptu. Zde diskutujeme Úvod do sloučení třídění v JavaScriptu a implementaci spolu s Vlastnosti. Další informace naleznete také v dalších navrhovaných článcích -
- Matematické funkce JavaScriptu
- Úvod do JavaScriptu
- Nejlepší Javascriptové rámce
- Nástroje JavaScript
- Top 6 algoritmů třídění v JavaScriptu