Úvod do matematických funkcí v C ++
Je obtížné a časově náročné, když musíte psát kód pokaždé, když v programu provádíte základní matematické výpočty. Proto C ++ poskytuje obrovské množství matematických funkcí, díky kterým je váš kód jednoduchý a efektivní. Pomocí matematických funkcí můžete na číslech provádět velké množství operací. Protože jsou tyto funkce vestavěny a podporovány knihovnou v C ++, je nutné zahrnout soubor záhlaví nebo na začátek kódu, aby bylo možné využívat všechny funkce matematických funkcí. Není třeba psát logiku v kódu, abyste mohli provádět operace, je to všechno v knihovně.
Různé typy matematických funkcí
C ++ poskytuje obrovské množství různých typů matematických funkcí uvedených níže s příklady:
1. Maximální a minimální funkce
- max (p, q): Vrátí maximální číslo mezi p a q.
- min (p, q): Vrátí minimální počet mezi p a q.
Kód C ++ pro implementaci výše uvedených funkcí
#include
#include
using namespace std;
int main() (
cout << max(16, 18) << "\n";
cout << min(16, 18) << "\n";
return 0;
)
Výstup:

2. Výkonové funkce
- pow (m, n): Vypočítá m zvýšené na sílu n.
- sqrt (m): Vypočítá druhou odmocninu m.
- cbrt (n): Vypočítá kořen krychle z n.
- hypotéza (m, n): Vypočte přepočet pravoúhlého trojúhelníku.
C ++ kód pro implementaci výše uvedených funkcí
#include
#include
using namespace std;
int main() (
cout << pow(2, 3) << "\n";
cout << sqrt(16) << "\n";
cout << cbrt(27) << "\n";
cout << hypot(3, 4) << "\n";
return 0;
)
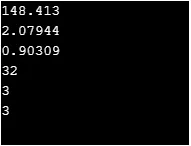
Výstup:

3. Exponenciální funkce
- exp (p): Vypočítá exponenciální e zvýšené na sílu p.
- log (p): Vypočítá logaritmus p.
- log10 (p): Vypočítá společný logaritmus p.
- exp2 (p): Vypočítá základ 2 exponenciál p.
- log2 (p): Vypočítá logaritmus základní 2 z p.
- logb (p): Vypočítá logaritmus p.
C ++ kód pro implementaci výše uvedených funkcí
#include
#include
using namespace std;
int main() (
cout << exp(5) << "\n";
cout << log(8) << "\n";
cout << log10(8) << "\n";
cout << exp2(5) << "\n";
cout << log2(8) << "\n";
cout << logb(8) << "\n";
return 0;
)
Výstup:
4. Celočíselné funkce
Pomáhá při hledání nejbližší celé hodnoty.
- ceil (z): zaokrouhlí nahoru hodnotu z.
- podlaha (z): zaokrouhlí dolů hodnotu z.
- round (z): Zaokrouhlí hodnotu z.
- fmod (z, y): Vypočítá zbytek divize z / y.
- trunc (z): Zaokrouhlí hodnotu z na nulu.
- rint (z): Zaokrouhlí hodnotu z za použití režimu zaokrouhlování.
- nearbyint (z): Zaokrouhlí hodnotu z na blízkou integrální hodnotu.
- zbytek (z, y): Vypočítá zbytek z / y.
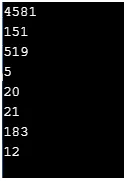
C ++ kód pro implementaci výše uvedených funkcí
#include
#include
using namespace std;
int main() (
cout << ceil(4580.01) << "\n";
cout << floor(151.999) << "\n";
cout << round(518.5) << "\n";
cout << fmod(5, 21) << "\n";
cout << trunc(20.25) << "\n";
cout << rint(21.25) << "\n";
cout << nearbyint(182.55) << "\n";
cout << remainder(12, 36) << "\n";
return 0;
)
Výstup:
5. Srovnávací funkce
Pomoc při porovnávání čísel v rychlém rozpětí nezáleží na tom, jak dlouho je číslo. Níže uvádíme několik příkladů porovnávacích funkcí:
- isgreater (p, q): Kontroluje, zda je p větší než q nebo ne.
- islessequal (p, q): Kontroluje, zda je p menší nebo rovno q nebo ne.
- isgreaterequal (p, q): Kontroluje, zda je p větší nebo rovno q nebo ne.
- islessgreater (p, q): Kontroluje, zda je p menší nebo větší než y nebo ne.
- isunordered (p, q): Kontroluje, zda je p porovnáno nebo ne.
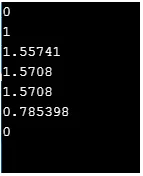
C ++ kód pro implementaci výše uvedených funkcí
#include
#include
using namespace std;
int main() (
// cout << less(22, 29) << "\n";
cout << isgreater(48, 47)<< "\n";
cout << islessequal(11, 5)<< "\n";
cout << isgreaterequal(19, 72)<< "\n";
cout << islessgreater(59, 84)<< "\n";
cout << isunordered(62, 84)<< "\n";
return 0;
)
Výstup:

6. Použití trigonometrické funkce
Funkce speciálně používané v geometrických výpočtech. Pravoúhlý trojúhelník dává vztah mezi úhlem k poměru délky obou stran.
- sin (y): Vypočítá hodnotu sinus y.
- cos (y): Vypočítá hodnotu cosine y.
- tan (y): Vypočítá hodnotu tečné y.
- asin (y): Vypočítá hodnotu inverzní sinus y.
- acos (y): Vypočítá hodnotu inverzní cosiny y.
- atan (y): Vypočítá hodnotu inverzní tangenty y.
- atan2 (y, x): Vypočítá hodnotu inverzní tangenty souřadnic y a x.
C ++ kód pro implementaci výše uvedených funkcí
#include
#include
using namespace std;
int main() (
cout << sin(0) << "\n";
cout << cos(0) << "\n";
cout << tan(1) << "\n";
cout << asin(1)<< "\n";
cout << acos(0)<< "\n";
cout << atan(1)<< "\n";
cout << atan2(0, 1)<< "\n";
return 0;
)
Výstup:
Zde jsou některé další zajímavé funkce, které pomohou při výpočtu hodnot hyperbolických trigonometrických funkcí a které se nazývají hyperbolické funkce.
- sinh (x): Vypočítá hodnotu hyperbolického sinu x.
- cosh (x): Vypočítá hodnotu hyperbolického kosinu x.
- tanh (x): Vypočítá hodnotu hyperbolického tangenta x.
- asinh (x): Vypočítá hodnotu hyperbolického oblouku sinus x.
- acosh (x): Vypočítá hodnotu kosbinu hyperbolického oblouku x.
- atanh (x): Vypočítá hodnotu hyperbolického oblouku sinus x.
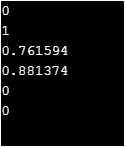
C ++ kód pro implementaci výše uvedených funkcí
#include
#include
using namespace std;
int main() (
cout << sinh(0)<< "\n";
cout << cosh(0)<< "\n";
cout << tanh(1)<< "\n";
cout << asinh(1)<< "\n";
cout << acosh(1)<< "\n";
cout << atanh(0)<< "\n";
return 0;
)
Výstup:
Závěr
Matematické funkce hrají důležitou roli při ukládání obrovského množství času a prostoru v paměti. Všechny funkce jsou vestavěny, není třeba implementovat přímo žádnou matematickou funkci pouze přidáním záhlaví souboru, který dává možnost použít celou knihovnu matematické třídy.
Doporučené články
Toto je průvodce matematickými funkcemi v C ++. Zde diskutujeme, že C ++ poskytuje příklady s velkým množstvím různých typů matematických funkcí. Můžete si také prohlédnout naše další doporučené články -
- Převažující v C ++
- Přetížení v C ++
- Druhá odmocnina v C ++
- Pole v C ++
- Přetížení v Javě
- Square Root v PHP
- Prvních 11 funkcí a výhod C ++
- Průvodce po Square Root v JavaScriptu