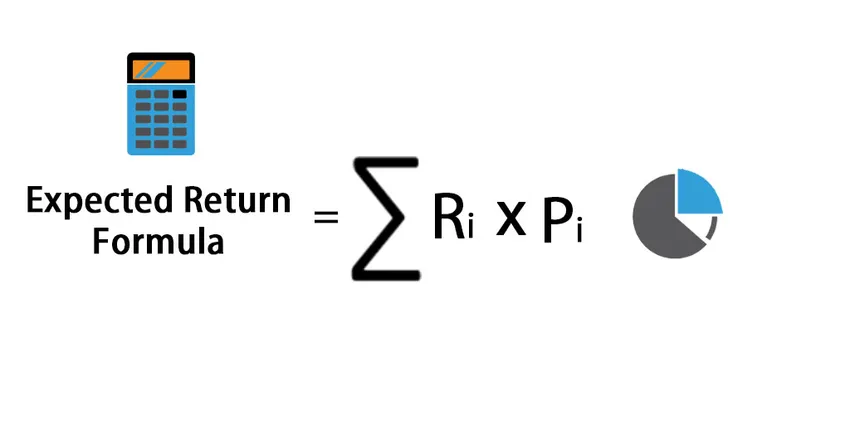
Vzorec očekávaného návratu (obsah)
- Očekávaný vzorec návratu
- Příklady vzorce očekávané návratnosti (se šablonou Excel)
- Očekávaná kalkulačka vzorce návratu
Očekávaný vzorec návratu
Očekávaný výnos lze definovat jako pravděpodobný výnos portfolia drženého investory na základě minulých výnosů nebo lze také definovat jako očekávanou hodnotu portfolia na základě rozdělení pravděpodobnosti pravděpodobných výnosů.
Zde je vzorec očekávaného návratu -
Expected Return = Expected Return=∑ (R i * P i )
Kde
- R i - Návratnost každého scénáře
- P i - Pravděpodobnost návratnosti v tomto scénáři
- i - Možné scénáře sahající od 1 do n
Příklady vzorce očekávané návratnosti (se šablonou Excel)
Vezměme si příklad, abychom lépe porozuměli výpočtu vzorce Očekávaný návrat.
Vzorec očekávaného návratu - Příklad č. 1
Vezměme si příklad portfolia akcií a dluhopisů, kde akcie mají 50% váhu a dluhopisy mají váhu 50%. Očekávaný výnos akcií je 15% a očekávaný výnos u dluhopisů je 7%.
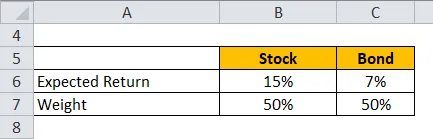
Očekávaný výnos se vypočítá pomocí vzorce uvedeného níže
Očekávaný výnos pro portfolio = Hmotnost zásoby * Očekávaný výnos pro skladem + Hmotnost dluhopisu * Očekávaný výnos pro dluhopis
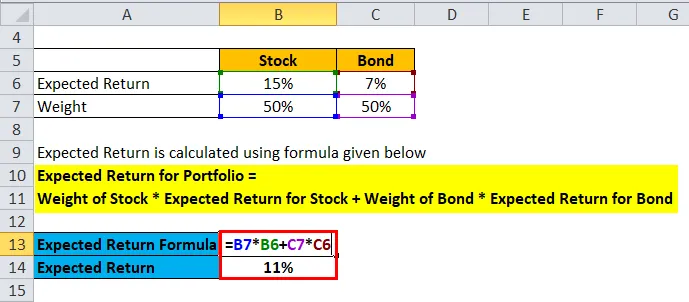
- Očekávaná návratnost portfolia = 50% * 15% + 50% * 7%
- Očekávaná návratnost portfolia = 7, 5% + 3, 5%
- Očekávaná návratnost portfolia = 11%
Vzorec očekávaného návratu - Příklad č. 2
Vezměme si příklad portfolia, které má akcie Reliance, Tata Steel, Eicher Motors a ITC.
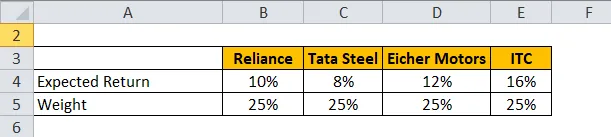
Očekávaný výnos se vypočítá pomocí vzorce uvedeného níže
Očekávaný výnos pro portfolio = ∑ Hmotnost každé akcie * Očekávaný výnos pro každou akcii

- Očekávaná návratnost portfolia = 25% * 10% + 25% * 8% + 25% * 12% + 25% * 16%
- Očekávaná návratnost portfolia = 2, 5% + 2% + 3% + 4%
- Očekávaná návratnost portfolia = 11, 5%
Vzorec očekávaného návratu - Příklad č. 3
Vezměme si příklad portfolia HUL, HDFC a desetiletého státního dluhopisu.
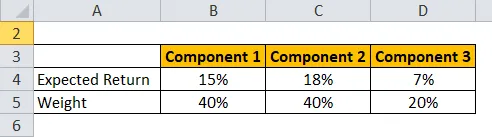
Očekávaný výnos se vypočítá pomocí vzorce uvedeného níže
Očekávaná návratnost portfolia = ∑ Hmotnost každé komponenty * Očekávaná návratnost každé komponenty
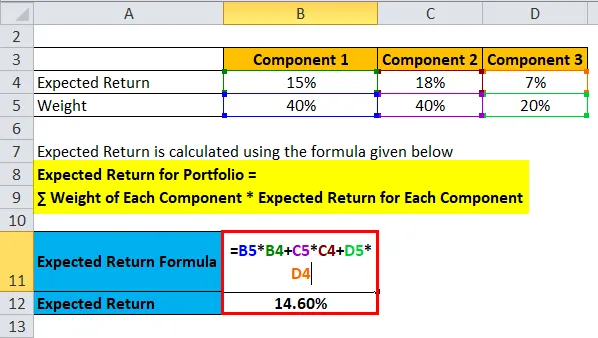
- Očekávaná návratnost portfolia = 40% * 15% + 40% * 18% + 20% * 7%
- Očekávaná návratnost portfolia = 6% + 7, 2% + 1, 40%
- Očekávaná návratnost portfolia = 14, 60%
Tuto šablonu Excel s očekávaným návratem můžete stáhnout zde - šablonu Excel s očekávaným návratem
Vysvětlení vzorce očekávaného návratu
Očekávaný výnos lze definovat jako pravděpodobný výnos portfolia drženého investory na základě minulých výnosů nebo lze také definovat jako očekávanou hodnotu portfolia na základě rozdělení pravděpodobnosti pravděpodobných výnosů. Očekávaný výnos lze v krátkodobém horizontu chápat jako náhodnou proměnnou, která může nabývat různých hodnot na základě určitých pravděpodobností. Tato náhodná proměnná má hodnoty v určitém rozmezí a může brát hodnoty pouze v tomto konkrétním rozsahu. Výpočet očekávaného výnosu je tedy založen na historických datech, a proto nemusí být spolehlivý při předpovídání budoucích výnosů. Lze na něj pohlížet jako na měřítko různých pravděpodobností a pravděpodobnosti dosažení pozitivní návratnosti investice a hodnoty této návratnosti.
Účelem tohoto je poskytnout investorovi představu o různých úrovních rizika, jaké jsou různé scénáře s různými pravděpodobnostmi, které přinášejí návratnost možná větší než bezrizikový výnos. Jak všichni víme, bezrizikovým výnosem by byl výnos vlády Spojených států za 10 let státních dluhopisů.
Relevance a použití vzorce očekávané návratnosti
Jak je uvedeno výše, výpočet očekávaného výnosu je založen na historických datech, a proto má omezení předpovídání budoucích možných výnosů. Investoři musí mít na paměti různé další faktory a neinvestovat na základě očekávané návratnosti vypočtené. Příklad: -
Portfolio A - 10%, 12%, -9%, 2%, 25%
Portfolio B - 9%, 7%, 6%, 6%, 12%
Pokud vezmeme v úvahu obě výše uvedená portfolia, obě mají očekávanou návratnost 8%, ale Portfolio A představuje velké riziko kvůli velké variabilitě výnosů. Investoři proto musí vzít v úvahu toto riziko, které se vypočítá pomocí takových opatření, jako je standardní odchylka a odchylka.
- Variance - Lze ji definovat jako variantu souboru datových bodů kolem jejich střední hodnoty. Vypočítá se na základě pravděpodobnosti váženého průměru čtvercových odchylek od průměru. Investoři musí brát v úvahu míru rizika.
První musí spočítat průměr všech návratů. Poté je zjištěna odchylka každého výnosu od hlavní hodnoty a na druhou je zajištěna veškerá pozitivní výsledky. A jakmile jsou na druhou, jsou násobeny příslušnými hodnotami pravděpodobnosti, aby zjistili rozptyl.
Rozptyl portfolia lze vypočítat z následujícího vzorce: - Pokud existují dvě portfolia A a B
Varianta portfolia = w A 2 * σ A 2 + w B 2 * σ B 2 + 2 * w A * w B * Cov (A, B)
Kde Cov (A, B) - je kovariance portfolií A a B
- Standardní odchylka - Je to další opatření, které označuje odchylku od jejího průměru. Standardní odchylka se vypočítá na základě druhé odmocniny rozptylu a označuje se σ.
Očekávaná kalkulačka vzorce návratu
Můžete použít následující kalkulačku očekávaného návratu.
| R 1 | |
| P 1 | |
| R2 | |
| P 2 | |
| R3 | |
| P 3 | |
| R4 | |
| P 4 | |
| Očekávaný návrat | |
| Očekávaný výnos = | R 1 * P 1 + R2 2 P 2 + R3 * P 3 + R4 * P 4 | |
| 0 * 0 + 0 * 0 + 0 * 0 + 0 * 0 = | 0 |
Závěr
Očekávaný výnos lze definovat jako pravděpodobný výnos portfolia drženého investory na základě minulých výnosů. Protože využívá pouze minulých výnosů, jedná se o omezení a hodnota očekávaného výnosu by neměla být jediným faktorem, který investoři zvažují při rozhodování, zda investovat do portfolia nebo ne. Je třeba zvážit i další opatření, jako je rozptyl portfolia a směrodatná odchylka.
Doporučené články
Toto byl průvodce vzorcem Očekávaný návrat. Zde diskutujeme, jak vypočítat očekávaný výnos spolu s praktickými příklady. Poskytujeme také očekávanou návratovou kalkulačku se stahovatelnou šablonou Excel. Další informace naleznete také v následujících článcích -
- Průvodce poměrem obratu aktiv
- Průvodce po vzorci nabídky Zeptejte se
- Jak vypočítat míru využití kapacity?
- Výpočet dluhopisového ekvivalentního výnosu
- Poměr obratu | Příklady | Šablona Excel