Perpetuity Formula (obsah)
- Trvalá formule
- Kalkulačka věčnosti
- Trvalá formulace v Excelu (se šablonou Excelu)
Trvalá formule
Trvalost lze označit za druh anuity, která dostává nespočetné množství pravidelných plateb. Na druhou stranu anuita obvykle znamená stálou platbu za finanční nástroj. Prvotním cílem vzorce věčnosti je znát současný a budoucí peněžní tok.
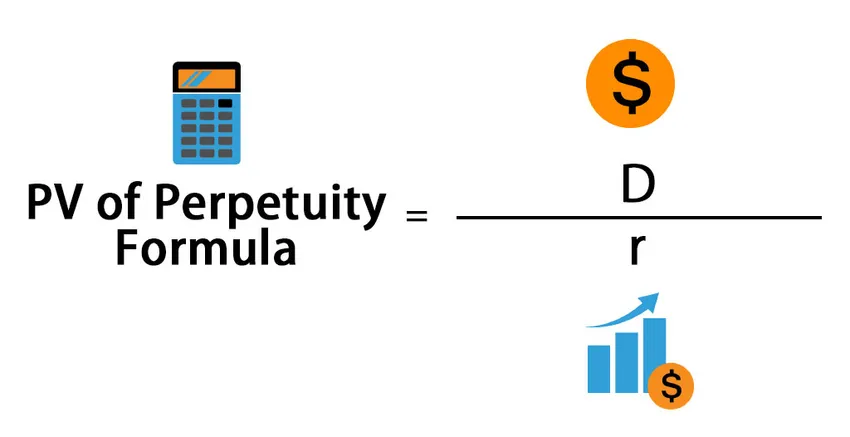
Zde je vzorec trvalosti -

Kde,
- PV = současná hodnota
- D = dividenda nebo kupón na období
- r = diskontní sazba
Nejobvyklejšími příklady vzorce trvalosti jsou případy, kdy jsou preferované akcie vydávány ve Velké Británii a ve většině případů, kdy obdržely dividendy dříve než dividendy akcionářů vlastního kapitálu a sazba dividend je pevně stanovena. Hodnota prioritních zásob tak může být vypočtena pomocí vzorce věčnosti pro nesčetný časový rámec.
Existuje další případ, kdy je možné změnit věčnost v závislosti na stejné platbě, ale na změně dividendové sazby. Pokud je diskontní sazba snížena, jmenovatel se rovněž sníží a hodnota bude mít tendenci se zvyšovat.
Příklad vzorce věčnosti
Osoba koupila dluhopis s kuponovou platbou 10 $ ročně a pokračuje po nekonečný časový rámec. Předpokládejme kupní diskontní sazbu 5%.
Tuto Perpetuity šablonu si můžete stáhnout zde - Perpetuity TemplatePoužíváme Perpetuity Formula, získáme -
- PV perpetuity = D / r
- PV perpetuity = 10 $ / 0, 05
- PV trvalosti = 200 $
Proto částka, kterou očekával, že zaplatí za tuto věčnost, bude 200 USD
Je třeba poznamenat, že ve výše uvedeném vzorci je časový rámec pevný.
Jak se odvozuje současný rostoucí vzorec?
Trvalá série, která roste z hlediska pravidelných plateb a je považována za neurčitou, která roste úměrně.
Proto lze vzorec shrnout takto:
PV = D / (1 + r) + D (1 + g) / (1 + r) 2 + D (1 + g) 2….
Trvalá série je považována za pokračování po nekonečné období. Vzorec lze znovu napsat a zobrazit jako následující příklad:
John investoval do dluhopisu, který mu platil kuponovou platbu na nekonečné období. Tato obligace vyplácí Johnovi 200 USD každý rok. Pokud předpokládáme, že diskontní sazba je 6%, kolik John by měl za tuto dluhopis zaplatit?
- Dividenda = 200
- Diskontní sazba = 0, 06
Používáme Perpetuity Formula, získáme -
- PV perpetuity = D / r
- PV perpetuity = 200 / 0, 06
- PV trvalosti = 3333, 33 $
Kupónová sazba je tedy 333, 33 USD, kterou John zaplatil při nákupu Dluhopisu.
Vlastnosti Perpetuity Formula
- Trvalost se nazývá anuita, která je nekonečná a nemá konec.
- Souvisí to s platbou v hotovosti, která trvá navždy.
- Je třeba zmínit konkrétní datum, od kterého věčnost začíná a má tendenci pokračovat do nekonečné budoucnosti.
PV = A / r
Kde,
PV představuje současnou hodnotu věčnosti
A představuje částku pravidelné platby
Současnou hodnotu věčnosti lze kromě toho určit také následujícími kroky:
Krok 1 Chcete-li najít roční platbu, úrokovou sazbu a míru trvalého růstu
Krok 2 Do vzorce vložte skutečné číslo
* Současná hodnota f \ growth perpetuity = P / (ig)
Pokud P představuje roční platbu, „i“ diskontní sazba
a 'g' je rychlost růstu.
Vysvětlení vzorce věčnosti
Má se za to, že vzorec trvalosti detekuje volný peněžní tok v terminálním roce provozu. Očekává se, že společnost nebo konkrétnější podnik bude pravděpodobně fungovat navždy. Z vzorce perpetuity se tedy předpokládá, že celková částka požadovaná při výplatě dividendy za nesčetné časové období.
Víme, že vzorec věčnosti je ve své podstatě teoretický, lze jej pochopit pomocí následujícího příkladu.
V případě obchodu s nemovitostmi, kdy jedna osoba koupí nemovitost a dá ji k pronájmu, pak má vlastník nárok na výdělek, který je nekonečně přirozený nebo jinými slovy se očekává, že příjem z nájemného bude plynout na nekonečný časový rámec. Předpokládáme, že majetek bude trvat nekonečný čas.
Význam a použití věčné formule
Jedním z rozporů ve věčném vzorci je jeho hodnota, která je v přírodě nekonečná.
Může existovat argument ohledně konečného ocenění konkrétního peněžního toku po nekonečný časový rámec. Odpověď může být dána takto
jak budoucí peněžní tok neustále klesá kvůli míře inflace, současné hodnoty jsou vysoké v prvních letech a hodnota věčnosti neustále klesá s časem. Mává skutečná hodnota plateb v průběhu času tendenci klesat? Takže velmi vzdálená budoucnost bude mít ocenění, které bude rovno nule, ale nebude to nulová hodnota. Proto vypočítáváme hodnotu nekonečných řad pomocí vzorce věčnosti.
V podnikových financích se hodnota jiného proudu peněžních toků v průběhu času liší. Trvalost není nic jiného než proud peněžních toků, které nikdy nekončí. Pokud tedy kupujeme věčnost, znamená to, že její splacení bude trvat do konce doby.
Pokud vezmeme v úvahu příklad kmenových akcií, všimneme si, že dividenda obdržená akcionáři je nekonečná, a proto držitel vlastního kapitálu získává nekonečný tok budoucí dividendy proti nákupu akcií.
Totéž platí pro studenty, kteří dostávají stipendium. Vzhledem k tomu, že stipendium se vyplácí za pevný počet let, jsou výsledky filantropických aktivit považovány za nekonečné budoucnosti.
Kalkulačka věčnosti
Můžete použít následující kalkulačku perpetuity
| D | |
| R | |
| PV z Perpetuity Formula = | |
| PV z Perpetuity Formula = |
|
|
Trvalá formulace v Excelu (se šablonou Excelu)
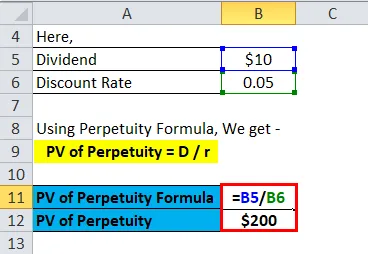
Zde uděláme stejný příklad vzorce Perpetuity v Excelu. Je to velmi snadné a jednoduché. Musíte zadat dva vstupy, tj. Dividendu a diskontní sazbu
Perpetuity můžete snadno spočítat pomocí vzorce v dodané šabloně.
Závěr
Obecnými předpoklady, které se berou v úvahu v případě trvalosti, je, že časový rámec je nekonečný. V praxi však existuje konečná hodnota současné hodnoty věčnosti, která se přirozeně zvyšuje a očekává se, že díky inflaci, která je brána v úvahu, dosáhne návratnosti, která má nízkou hodnotu.
Může však nastat situace, kdy se hodnota věčnosti může změnit v průběhu časového období, včetně stejného počtu plateb. K tomu obvykle dochází v důsledku změny diskontní nebo kuponové sazby. Hodnota trvalosti roste se snížením kuponové sazby a naopak.
Doporučené články
Toto byl průvodce po vzorci věčnosti. Zde diskutujeme jeho použití spolu s praktickými příklady. Rovněž vám poskytneme kalkulačku trvalosti se šablonou Excel ke stažení. Další informace naleznete také v následujících článcích -
- Míra využití kapacity Šablona Excel
- Vypočítat průběžné složení pomocí vzorce
- Průvodce po vzorci multiplikátoru vlastního kapitálu
- Příklady vzorce marže provozního zisku