
Rozpětí odchylky (obsah)
- Rozpětí odchylky
- Příklady rozpětí chyb (se šablonou Excel)
- Rozpětí kalkulačky chyb
Rozpětí odchylky
Ve statistice vypočítáváme interval spolehlivosti, abychom zjistili, kde bude klesat hodnota dat statistik vzorku. Rozsah hodnot, které jsou pod a nad statistikou vzorku v intervalu spolehlivosti, se nazývá Margin of Error. Jinými slovy, v podstatě jde o míru chyby ve statistice vzorku. Čím vyšší je míra chyb, tím menší bude důvěra ve výsledky, protože míra odchylek v těchto výsledcích je velmi vysoká. Jak název napovídá, míra chyby je rozsah hodnot nad a pod skutečnými výsledky. Pokud například dostaneme odpověď v průzkumu, v němž 70% lidí odpovědělo „dobře“ a míra chyb je 5%, znamená to, že obecně si 65% až 75% populace myslí, že odpověď je „dobrá“. .
Vzorec pro Margin of Error -
Margin of Error = Z * S / √n
Kde:
- Skóre Z - Z
- S - standardní odchylka populace
- n - Velikost vzorku
Další vzorec pro výpočet míry chyby je:
Margin of Error = Z * √((p * (1 – p)) / n)
Kde:
- p - Poměr vzorku (zlomek vzorku, který je úspěšný)
Nyní, abyste našli požadované z skóre, musíte znát interval spolehlivosti vzorku, protože na tom závisí Z skóre. Níže uvedená tabulka uvádí vztah intervalu spolehlivosti a skóre z:
| Interval spolehlivosti | Z - Skóre |
| 80% | 1, 28 |
| 85% | 1, 44 |
| 90% | 1, 65 |
| 95% | 1, 96 |
| 99% | 2, 58 |
Jakmile znáte interval spolehlivosti, můžete použít odpovídající hodnotu z a odtud vypočítat míru chyby.
Příklady rozpětí chyb (se šablonou Excel)
Vezměme si příklad, abychom lépe porozuměli výpočtu Margin of Error.
Tuto šablonu Margin of Error si můžete stáhnout zde - Margin of Error TemplateRozpětí chyby vzorec - příklad # 1
Řekněme, že provádíme průzkum, abychom zjistili, jaké je skóre, které získávají studenti vysokých škol. Náhodně jsme vybrali 500 studentů a požádali jsme o jejich hodnocení. Průměr toho je 2, 4 ze 4 a standardní odchylka je 30%. Předpokládejme, že interval spolehlivosti je 99%. Vypočtěte rozpětí chyby.
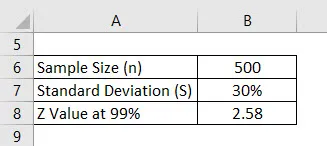
Řešení:
Rozpětí chyby se vypočítá pomocí vzorce uvedeného níže
Rozpětí chyby = Z * S / √n
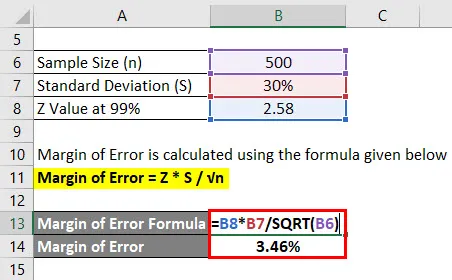
- Rozpětí chyby = 2, 58 * 30% / √ (500)
- Rozpětí chyby = 3, 46%
To znamená, že s 99% jistotou je průměrná známka studentů 2, 4 plus mínus 3, 46%.
Rozpětí chyby vzorec - Příklad # 2
Řekněme, že uvádíte na trh nový produkt pro zdraví, ale jste zmatení, jakou chuť budou mít lidé rádi. Jste zmateni mezi banánovou příchutí a vanilkovou příchutí a rozhodli jste se provést průzkum. Vaše populace na to je 500 000, což je váš cílový trh, a z toho jste se rozhodli zeptat na názor 1000 lidí, a to bude vzorek. Předpokládejme, že interval spolehlivosti je 90%. Vypočtěte rozpětí chyby.
Řešení:
Jakmile je průzkum dokončen, dozvěděli jste se, že 470 lidí má chuť banánů ráda a 530 požádalo o vanilkovou chuť.
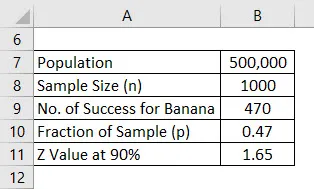
Rozpětí chyby se vypočítá pomocí vzorce uvedeného níže
Rozpětí chyby = Z * √ ((p * (1 - p)) / n)
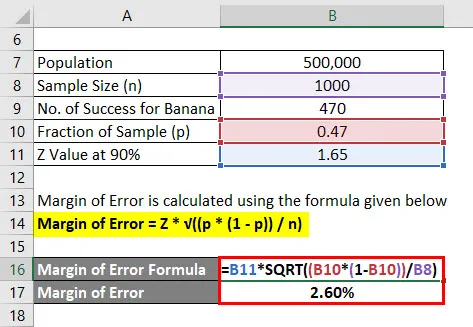
- Rozpětí chyby = 1, 65 * √ ((0, 47 * (1 - 0, 47)) / 1000)
- Rozpětí chyby = 2, 60%
Můžeme tedy říci, že s 90% jistotou, že 47% všech lidí mělo chuť banánů plus nebo mínus 2, 60%.
Vysvětlení
Jak je uvedeno výše, míra chyb nám pomáhá pochopit, zda je velikost vzorku vašeho průzkumu vhodná či nikoli. V případě, že je chyba okraje příliš velká, může se stát, že naše velikost vzorku je příliš malá a musíme ji zvýšit, aby výsledky vzorků lépe odpovídaly výsledkům populace.
Existují některé scénáře, kde se míra chyb nebude příliš používat a nepomůže nám při sledování chyby:
- Nejsou-li otázky průzkumu navrženy a nepomáhají získat požadovanou odpověď
- Pokud mají lidé, kteří na průzkum reagují, zaujatost ohledně produktu, pro který je průzkum prováděn, pak také výsledek nebude příliš přesný
- Pokud je vybraný vzorek sám řádným představitelem populace, v tomto případě také budou výsledky daleko.
Velkým předpokladem je také to, že populace je normálně distribuována. Takže pokud je velikost vzorku příliš malá a rozdělení populace není normální, skóre z nelze vypočítat a nebudeme moci najít chybu.
Relevance a použití marže chyby vzorce
Kdykoli použijeme vzorová data k nalezení nějaké relevantní odpovědi pro soubor populace, existuje určitá nejistota a šance, že by se výsledek mohl lišit od skutečného výsledku. Rozpětí chyby nám řekne, že jaká je úroveň odchylky, je, že existuje výstup vzorku. Musíme minimalizovat míru chyb, aby naše výsledky ukázek zobrazovaly skutečný příběh údajů o populaci. Čím nižší je míra chyb, tím lepší budou výsledky. Rozpětí chyb doplňuje a doplňuje statistické informace, které máme. Například pokud průzkum zjistí, že 48% lidí dává přednost víkendu doma, nemůžeme být tak přesní a v těchto informacích jsou některé chybějící prvky. Když jsme zde uvedli meze chyb, řekněme 5%, výsledek se bude interpretovat, protože 43-53% lidem se líbil nápad být doma o víkendu, což dává úplný smysl.
Rozpětí kalkulačky chyb
Můžete použít následující kalkulačku marže chyb
| Z | |
| S | |
| √n | |
| Rozpětí chyby | |
| Rozpětí chyby | = |
|
|
Doporučené články
Toto byl průvodce vzorcem Margin of Error. Zde diskutujeme, jak vypočítat Margin of Error spolu s praktickými příklady. Poskytujeme také kalkulačku Margin of Error s šablonou Excel ke stažení. Další informace naleznete také v následujících článcích -
- Průvodce po rovnici odpisování přímky
- Příklady vzorce zdvojnásobení času
- Jak vypočítat amortizaci?
- Vzorec pro centrální limitní teorém
- Skóre Altman Z | Definice Příklady
- Odpisový vzorec Příklady se šablonou Excel