
Úvod do matematických funkcí v C
Tento článek uvádí různé matematické funkce používané v programovacích jazycích C s ilustrací pracovního kódu. Počítače provádějí obrovské matematické výpočty a analýzy obrovských čísel. K tomu jsme použili matematické funkce v C. Než začneme, musíme vědět, že jazyky C používají záhlaví / knihovnu Math.h pro různé matematické funkce. To pomáhá při výpočtu trigonometrických operací, logaritmů, absolutních hodnot, druhých odmocnin. Pojďme tedy prozkoumat různé typy funkcí používaných v této knihovně. Všechny tyto funkce se zdvojnásobí jako datový typ a vrátí se stejně.
Různé matematické funkce v C
Podívejme se na různé funkce definované v math.h a matematická knihovna je rozdělena do tří hlavních typů: Trigonometrické funkce, matematické funkce, Log / expo funkce. K implementaci níže uvedených funkcí je nutné zahrnout nebo do kódu.
1. patro (double a)
Tato funkce vrací největší celočíselnou hodnotu, která není větší než hodnota „a“. Zaokrouhlí hodnotu a jako výsledek vrátí dvojnásobek. Chová se jinak pro záporná čísla, protože se zaokrouhlí na další záporné číslo.
Příklad: podlaha (7.2) je 7, 0
podlaha (-7, 2) je -8, 0
Příklad:
Tento program ukazuje, jak vypočítat podlahu pro deklarovanou hodnotu a zaokrouhlí se na další hodnotu 10.
#include
#include
int main()
(
double f= -9.33;
int final;
final = floor(f);
printf("Floor value of %.2f = %d", f, final);
return 0;
)
Výstup:

2. ceil ()
Syntax:
double ceil (double b)
Tato funkce vrací nejmenší celé číslo, které je větší nebo rovno b a zaokrouhlí hodnotu nahoru. Pro zápornou hodnotu se pohybuje směrem doleva. Příklad 3.4 vrátí -3 má výstup.
Příklad:
Tento program vysvětluje převzetím vstupu do argumentu float a vrací hodnotu stropu.
#include
#include
int main()
(
float n, ceilVal;
printf(" Enter any Numeric element : ");
scanf("%f", &n);
ceilVal = ceil(n);
printf("\n The Value of %.2f = %.4f ", n, ceilVal);
return 0;
)
Výstup:

3. Sqrt ()
Tato funkce vrací druhou odmocninu zadaného čísla.
Syntax:
sqrt( arg)
Příklad:
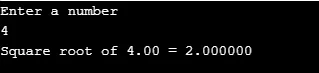
Níže uvedený kód vysvětluje nejznámější matematickou funkci sqrt () pomocí hodnot „n“ pro výpočet druhé odmocniny pro různé hodnoty „n“.
#include
#include
int main()
(
double n, output;
printf("Enter a number\n");
scanf("%lf", &n);
output = sqrt(n);
printf("Square root of %.2lf = %f", n, output);
return 0;
Výstup:
4. kolo ()
Tato funkce zaokrouhlí nejbližší hodnotu daného vstupu. Vyhodí chybu, pokud je hodnota příliš velká. Ostatní funkce jako lround (), llround () také zaokrouhlí nejbližší celé číslo.
Syntax:
int round(arg)
Příklad:
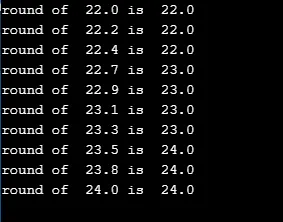
Níže uvedený kód je velmi jednoduchý a zaokrouhlí se na nejbližší hodnotu „r“ ve smyčce for.
#include
#include
int main ()
(
for(double r=110;r<=120;r+=1.1)
printf("round of %.1lf is %.1lf\n", r/5.0, round(r/5.0));
return 0;)
Výstup:
5.pow ()
Tato funkce se vrátí k napájení pro dané číslo (a b ). Vrací zvýšenou hodnotu na mocninu b, která má dva základní parametry a exponent.
Příklad:
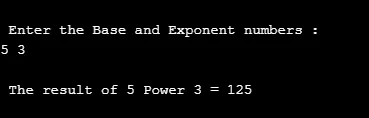
Ve zdrojovém kódu níže umožňujeme uživateli zadat vstupní hodnotu pro výpočet síly daných dvou argumentů.
#include
#include
int main()
(
int r, ba, expr;
printf("\n Enter the Base and Exponent numbers : \n");
scanf("%d %d", &ba, &expr);
r = pow(ba, expr);
printf("\n The result of %d Power %d = %d ", ba, expr, r);
return 0;
)
výstup:
6. trun ()
Tato funkce pomáhá při zkrácení dané hodnoty. Vrací celočíselné hodnoty. Pro zkrácení plovoucí a dvojité hodnoty jsou použity truncf (), truncl ().
Syntax:
double trunc(a);
Příklad:
Pod zdrojovým kódem jsou dvě vstupní hodnoty a, b pro zkrácení dvojitých hodnot.
#include
#include
void main() (
double m, n, a, b;
a = 56.16;
b = 85.74;
m = trunc(a);
n = trunc(b);
printf("The value of a: %lf\n", m);
printf("The value of a: %lf\n", n);
)
Výstup:

7. fmod ()
Tato funkce vrací zbytek pro dané dvě vstupní hodnoty, když m je vyděleno n.
Syntax:
double fmod(double I, double j)
Příklad:
V níže uvedeném příkladu trvá, než uživatel vypočítá zbytek pomocí funkce fmod (), dvě hodnoty.
#include
#include
int main()(
double fiN;
double secN;
double n;
printf("Enter the first number : ");
scanf("%lf", &fiN);
printf("Enter the second number : ");
scanf("%lf", &secN);
printf("fmod(firstNumber, secondNumber) is %lf \n", fmod(fiN, secN));
)
Výstup:

Trigonometrické funkce
Níže jsou uvedeny různé funkce Trigonometrické:
1. hřích ()
Tato vestavěná funkce poskytuje sinusovou hodnotu daného čísla, počítá hodnoty s pohyblivou řádovou čárkou. asin () počítá oblouk, pro hyperbolický je to sinh ().
Syntax:
return type sin(y);
y vrací hodnotu v radiánech a typ návratu se zdvojnásobí.
Příklad:
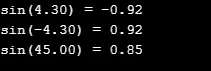
V následujícím zdrojovém kódu jsem vzal dvě různé vstupní hodnoty pro výpočet hodnoty sin a vrátí se dvakrát.
#include
#include
int main()
(
double a;
double z;
a = 4.3;
z = sin(a);
printf("sin(%.2lf) = %.2lf\n", a, z);
a = -4.3;
z = sin(a);
printf("sin(%.2lf) = %.2lf\n", a, z);
a = 45;
z = sin(a);
printf("sin(%.2lf) = %.2lf\n", a, z);
return 0;
)
Výstup:
2. sinh ()
Tato matematická funkce vypočítá trigonometrickou tangenciální sinusovou hodnotu pro dané číslo.
Syntax:
double sinh(x);
Příklad
V níže uvedeném zdrojovém kódu je Sine hyperbolic vypočítán deklarováním vstupní hodnoty.
#include
#include
#define PI 3.141592654
int main()
(
double gt = 3.60, z;
z = sinh(gt);
printf("Sine hyperbolic of %.2lf is = %.2lf", gt, z);
return 0;
)
Výstup

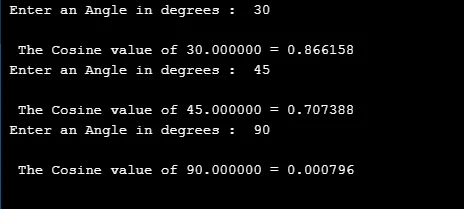
3. cos ()
Tato matematická funkce určuje trigonometrickou kosinovou hodnotu pro daný prvek.
Syntaxe: return type cos(argument);
#include
#include
#define PI 3.14
int main()
(
double cVal, rVal, dVal;
for(int i=0;i<=2;i++)
(
printf(" Enter an Angle in degrees : ");
scanf("%lf", &dVal);
rVal = dVal * (PI/180);
cVal = cos(rVal);
printf("\n The Cosine value of %f = %f ", dVal, cVal);
printf("\n");
)
return 0;
)
Výstup:
4. cosh ()
Vrací hyberbolický kosinus pro danou hodnotu.
Syntax:
double cosh(y);
Příklad
Níže uvedený příklad ukazuje, že výpočet dvou hyperbolických hodnot vyžaduje dvě různé vstupní hodnoty.
#include
#include
int main ()
(
double k, r;
k = 0.6;
r = cosh(k);
printf("Hyperbolic cosine of %lf is = %lf\n", k, r);
k = -0.8;
r = cosh(k);
printf("Hyperbolic cosine of %lf is = %lf\n", k, r);
return 0;)
Výstup

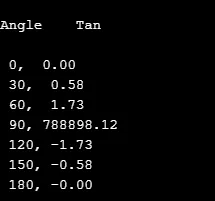
5. tan ()
Tato matematická knihovna počítá tečné hodnoty úhlu pro matematický výraz a měřené v radiánech.
Může být deklarována jako
double tan(arguments);
Příklad
V následujícím zdrojovém kódu se hodnota tan vypočítá pro následující úhly, které se zvyšují pomocí smyčky.
# include
# include
# include
void main()
(
float z ;
int k ;
char ch ;
printf("\nAngle \t Tan \n") ;
for (k = 0; k <= 180; k = k + 30)
(
z = k * 3.14159 / 180 ;
printf("\n %d, %5.2f", k, tan(z));
)
getch() ;
)
Výstup:
6. tanh ()
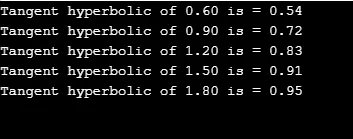
Funkce tanh () vrací hyperbolický tangens dané hodnoty. Vyžaduje jeden parametr. Kromě hledání tangens pro dlouhé dvojité a float tanhl () a tanhf () se používají pro výpočet.
Syntax:
double tanh( val);
Příklad:
Tečná hyberbolika se počítá pro hodnoty „j“ pro smyčky. Uvidíme, jak to funguje.
#include
#include
#define PI 3.141592654
int main()
(
double val, r;
for(double j=0.60; j<=2.0;j+=.30)
(
r = tanh(j);
printf("Tangent hyperbolic of %.2lf is = %.2lf", j, r);
printf("\n");
)
return 0;
)
Výstup:
Protokolovat aritmetické funkce
Níže jsou uvedeny různé funkce log aritmetiky:
1. exp ()
Tato funkce provádí výpočet exponenciálu pro danou hodnotu (e x ). Existují také jiné podtypy, jako je frexp (), Idexp () vracející mantisu a vynásobené silou x.
Syntax:
return type exp(value);
Příklad:
Program vezme od uživatele číselnou hodnotu pro výpočet exponentu pro danou hodnotu a vrátí dvojnásobek.
#include
#include
int main()
(
double numb, eVal;
printf(" Enter any Numeric Value : ");
scanf("%lf", &numb);
eVal = exp(numb);
printf("\n Exponential Value of e power %lf = %lf ", numb, eVal);
printf("\n");
return 0;
)
Výstup

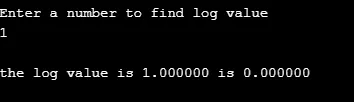
2. log ()
Tato funkce vrací logaritmickou hodnotu daného čísla. (na základní e. log e )
Syntax:
double log(arg);
Příklad:
V následujícím příkladu je hodnota logu pro dané číslo vypočítána pomocí funkce. Uživatelem definovaná funkce lgm () provádí výpočet a funkce se nazývá hlavní funkce.
#include
#include
float lgm ( float iv );
int main ()
(
float q, r ;
printf ( "\nEnter a number to find log value \n");
scanf ( "%f", &q ) ;
r = lgm ( q ) ;
printf ( "\nthe log value is %f is %f", q, r );
)
float lgm ( float iv ) // function definition
(
float exe ;
exe = log(iv);
return ( exe ) ;
)
výstup:
Závěr
Na závěr jsme viděli různé matematické funkce používané v programování v C a to jsou přímé knihovnické funkce, které je třeba použít. Programy C tyto funkce využívají pro různé matematické operace. Při řešení některých složitých verzí výpočtů má tato vestavěná funkce výhodu matematicky orientovaného programovacího jazyka, který vrací jednoduché hodnoty.
Doporučené články
Toto je průvodce matematickými funkcemi v C. Zde diskutujeme různé matematické funkce v C s příklady. Můžete si také prohlédnout naše další doporučené články -
- Matematické funkce PHP
- Matematické funkce JavaScriptu
- Přenos funkcí v Matlabu
- Funkce řetězce JavaScriptu
- Úvod do matematických funkcí v Pythonu
- Přehled matematických funkcí v C #
- C Programovací násobení matic
- Square Root v PHP
- Příklady Square Root v JavaScriptu