Efektivní roční sazba vzorce (obsah)
- Vzorec
- Příklady
- Kalkulačka
Co je vzorec efektivní roční sazby?
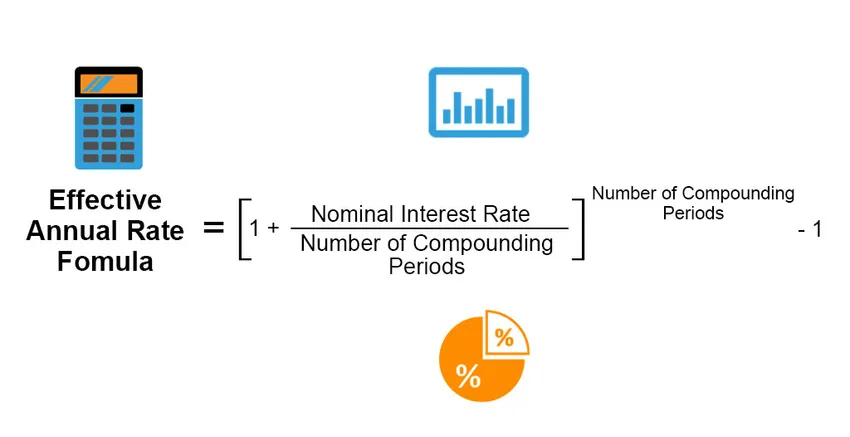
Efektivní roční sazba je skutečná úroková sazba, která je získána nebo vyplacena z investice, úvěru nebo jakéhokoli podobného finančního produktu, a je jinak odlišná od „nominální úrokové sazby“ kvůli výplatnímu období úroků, složení úrokové sazby, celkem časové období půjčky nebo investice atd. Efektivní roční sazba se vypočítá podle následujícího vzorce;
Effective Annual Rate = ((1 + (Nominal Interest Rate / Number of Compounding Periods)) Number of Compounding Periods) – 1
Příklady vzorce efektivní roční sazby (se šablonou Excel)
Vezměme si příklad, abychom lépe porozuměli výpočtu efektivní roční sazby.
Tuto šablonu efektivní roční sazby vzorce Excel si můžete stáhnout zde - šablonu efektivní roční sazby vzorce ExcelVzorec efektivní roční sazby - Příklad č. 1
Předpokládejme, že pan X si vezme osobní půjčku od banky s úrokovou sazbou 20%, která se každoročně sčítá. Vypočítejte efektivní roční sazbu pomocí těchto informací.

Řešení:
Efektivní roční sazba se vypočítá pomocí vzorce uvedeného níže
Efektivní roční sazba = ((1 + (nominální úroková sazba / počet kombinovaných období)) Počet kombinovaných období) - 1

- Efektivní roční míra = ((1 + (20% / 2)) 2) - 1
- Efektivní roční sazba = 21%
Vzorec efektivní roční sazby - Příklad č. 2
Předpokládejme, že pan A investoval 100 USD do depozitního certifikátu, který vyplácí nominální roční úrokovou sazbu 10%, která se zvyšuje čtvrtletně. Vypočítejte efektivní roční sazbu.

Řešení:
Efektivní roční sazba se vypočítá pomocí vzorce uvedeného níže
Efektivní roční sazba = ((1 + (nominální úroková sazba / počet kombinovaných období)) Počet kombinovaných období) - 1
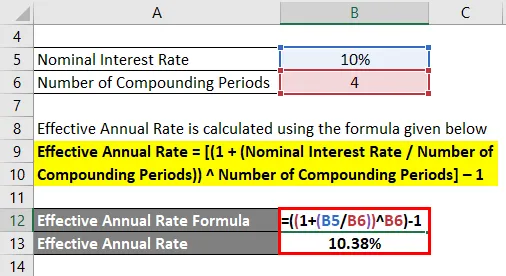
- Efektivní roční míra = ((1 + (10% / 4)) 4) - 1
- Efektivní roční sazba = 10, 38%
Vzorec efektivní roční sazby - Příklad č. 3
Předpokládejme, že investice do podílových fondů vyvolávají roční výnosovou úrokovou sazbu 15, 50%, zatímco P2P půjčování vydělává 15% roční nominální úrokovou sazbu, složenou měsíčně. Vypočítejte tedy efektivní roční sazbu pro oba případy.

Řešení:
Efektivní roční sazba se vypočítá pomocí vzorce uvedeného níže
Efektivní roční sazba = ((1 + (nominální úroková sazba / počet kombinovaných období)) Počet kombinovaných období) - 1
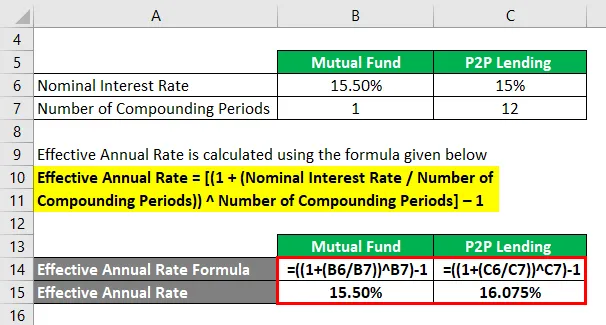
Pro podílový fond
- Efektivní roční míra = ((1 + (15, 50% / 1)) 1) - 1
- Efektivní roční sazba = 15, 50%
Pro půjčování P2P
- Efektivní roční míra = ((1 + (15% / 12)) 12) - 1
- Efektivní roční sazba = 16, 075%
Vysvětlení
Nominální úroková sazba je uvedená sazba finančního produktu. V příkladu 3 nominální sazba zobrazená na produktech způsobuje, že vzájemný fond vypadá jako upřednostňovaná volba investic pro investory kvůli 0, 50% vyšší roční nominální úrokové úrokové sazbě.
Efektivní roční sazba se však vypočítá tak, že se vezme nominální roční úroková sazba a složí se pro počet stanovených období (12, pokud je složení měsíční; 6, pokud je složení jednou za dva měsíce; 4, pokud je čtvrtletní, a 2, pokud je je pololetní) použitelné v časovém rozpětí jednoho roku. V případě podílového fondu je počet kombinovaných období za rok 1, zatímco v případě půjček P2P je to měsíční kombinování, proto existuje 12 kombinovaných období.
Na základě vzorce
Efektivní roční výnosy = ((1 + (nominální úroková sazba / počet kombinovaných období)) (počet kombinovaných období)) - 1
Efektivní roční výnos podílového fondu = ((1 + (15, 50% / 1)) 1) - 1 = 15, 50%
Efektivní roční výnos z půjček P2P = ((1 + (15, 00% / 12)) 12) - 1 = 16, 075%
Relevance a použití vzorce efektivní roční sazby
Vzorec efektivní roční sazby se používá k rozlišení skutečné IRR (Interní míra návratnosti) nebo anualizovaného výnosu pro úrokovou sazbu, která se může nebo nemusí v daném období vícekrát složit. To by se dalo velmi dobře použít při porovnávání různých druhů investičních příležitostí nebo půjček poskytnutých v různých strukturách.
Předpokládejme, že existují 2 investiční příležitosti, termínované vklady pošta a fixní vklady, na které se investor zúžil, vzhledem k jeho rizikové chuti a vhodnosti. Konečným cílem investora je z těchto vkladů vytěžit maximum a dosáhnout vyšší návratnosti. Oba nástroje však nabízejí poněkud odlišné úrokové sazby, zatímco termínovaný vklad pošta nabízí čtvrtletní kompilaci za uvažované období.
- Investiční částka: Rs. 10 lakhů
- Investiční období: 5 let
- Bankovní fixní vklad: 7, 5% roční úrok
- Termínovaný vklad pošta: 7, 4% roční úrok, složený čtvrtletně
Z pohledu nabízených ročních úrokových sazeb se zdá, že nejlepší možností je pevný vklad banky. Pokud však investor skutečně vypočítá čtvrtletní faktor složení termínovaného vkladu poštovního úřadu, výsledkem bude efektivní roční sazba / výnos 7, 61%.
Díky této malé změně efektivní sazby ze 7, 4% na 7, 61% by investor vydělal celkem Rs. 4, 42, 848, 28 z tohoto konkrétního nástroje, zatímco on / ona by vydělala Rs. 3, 35, 469, 14 z nástroje pevného vkladu banky.
Pokud by investor nechal vypočítat tuto efektivní roční sazbu, ztratil by příležitost získat přibližně více než Rs. 1 lakh z jeho investice.
Efektivní kalkulačka ročních sazeb
Můžete použít následující efektivní roční kalkulačku sazeb
| Nominální úroková sazba | |
| Počet kombinovaných období | |
| Efektivní roční míra | |
| Efektivní roční míra | ((1 + (nominální úroková sazba / počet období zkompletování)) Počet období zkompletování ) - 1 | |
| ((1 + (0/0)) 0 ) - 1 = | 0 |
Doporučené články
Toto je průvodce vzorcem efektivní roční sazby. Zde diskutujeme, jak vypočítat efektivní roční sazbu, spolu s praktickými příklady. Poskytujeme také efektivní roční kalkulačku sazeb se stahovatelnou šablonou Excel. Další informace naleznete také v následujících článcích -
- Kalkulačka pro reálnou úrokovou sazbu
- Návratnost kapitálové emise | Definice
- Jak vypočítat efektivní úrokovou sazbu?
- Co je současná hodnota vzorce anuity?