Rozdíl mezi lineární regresí vs. logickou regresí
Následující článek Lineární regrese vs. Logistická regrese poskytuje nejdůležitější rozdíly mezi oběma, ale než uvidíme, co znamená regrese?
Regrese
Regrese je v podstatě statistické měřítko pro stanovení síly vztahu mezi jednou závislou proměnnou, tj. Výstupem Y a řadou dalších nezávislých proměnných, tj. X 1, X 2 atd. Regresní analýza se v zásadě používá pro predikci a prognózu.
Co je lineární regrese?
Lineární regrese je algoritmus, který je založen na supervizované oblasti učení strojového učení. Zdědí lineární vztah mezi svými vstupními proměnnými a jedinou výstupní proměnnou, kde je výstupní proměnná svou povahou spojitá. Používá se k predikci hodnoty výstupu, řekněme Y ze vstupů, řekněme X. Když se uvažuje pouze o jednom vstupu, nazývá se to jednoduchá lineární regrese.
Lze ji rozdělit do dvou hlavních kategorií:
1. Jednoduchá regrese
Princip činnosti: Hlavním cílem je zjistit rovnici přímky, která nejlépe odpovídá vzorkovaným datům. Tato rovnice algebraicky popisuje vztah mezi oběma proměnnými. Nejvhodnější přímka se nazývá regresní čára.
Y = β 0 + β 1 X
Kde,
β představuje funkce
p 0 představuje přestávku
p 1 představuje koeficient funkce X
2. Multivariabilní regrese
Používá se k predikci korelace mezi více než jednou nezávislou proměnnou a jednou závislou proměnnou. Regrese s více než dvěma nezávislými proměnnými je založena na tvaru přizpůsobení konstelaci dat na vícerozměrném grafu. Tvar regrese by měl být takový, aby minimalizoval vzdálenost tvaru od každého datového bodu.
Lineární vztahový model lze matematicky znázornit takto:
Y = β 0 + β 1 X 1 + β 2 X 2 + β 3 X 3 + ……. + β n X n
Kde,
β představuje funkce
p 0 představuje přestávku
pi představuje koeficient funkce X1
β n představuje koeficient funkce X n
Výhody a nevýhody lineární regrese
Níže jsou uvedeny výhody a nevýhody:
Výhody
- Vzhledem ke své jednoduchosti se široce používá pro predikce a závěry.
- Zaměřuje se na analýzu dat a předzpracování dat. Jedná se tedy o různá data, aniž by se trápily detaily modelu.
Nevýhody
- Funguje to efektivně, když jsou data normálně distribuována. Pro efektivní modelování je tedy třeba zabránit kolinearitě.
Co je to Logistická regrese?
Je to forma regrese, která umožňuje predikci diskrétních proměnných směsí spojitých a diskrétních prediktorů. Výsledkem je jedinečná transformace závislých proměnných, která ovlivňuje nejen proces odhadování, ale také koeficienty nezávislých proměnných. Řeší stejnou otázku, jakou vícenásobná regrese dělá, ale bez distribučních předpokladů pro prediktory. V logistické regresi je výsledná proměnná binární. Účelem analýzy je posoudit účinky více vysvětlujících proměnných, které mohou být číselné nebo kategorické nebo obojí.
Druhy logistické regrese
Níže jsou uvedeny dva typy logistické regrese:
1. Binární logická regrese
Používá se, když závislá proměnná je dichotomická, tj. Jako strom se dvěma větvemi. Používá se, když závislá proměnná není parametrická.
Používá se, když
- Pokud neexistuje linearita
- Existují pouze dvě úrovně závislé proměnné.
- Pokud je pochybnost vícerozměrné normality.
2. Multinomiální logistická regrese
Multinomiální logická regresní analýza vyžaduje, aby nezávislé proměnné byly metrické nebo dichotomické. Pro nezávislé proměnné neprovádí žádné předpoklady linearity, normality a homogenity rozptylu.
Používá se, když závislá proměnná má více než dvě kategorie. Používá se k analýze vztahů mezi nemetrickými závislými proměnnými a metrickými nebo dichotomickými nezávislými proměnnými, poté porovnává více skupin kombinací binárních logistických regresí. Nakonec poskytuje sadu koeficientů pro každé ze dvou srovnání. Koeficienty pro referenční skupinu se považují za všechny nuly. Nakonec je predikce prováděna na základě nejvyšší pravděpodobnosti.
Výhoda logistické regrese: Jedná se o velmi efektivní a široce používanou techniku, protože nevyžaduje mnoho výpočetních zdrojů a nevyžaduje žádné vyladění.
Nevýhoda logistické regrese: Nelze ji použít pro řešení nelineárních problémů.
Srovnání hlava-hlava mezi lineární regresí proti logistické regresi (infografika)
Níže je uvedeno šest největších rozdílů mezi lineární regresí a logistickou regresí 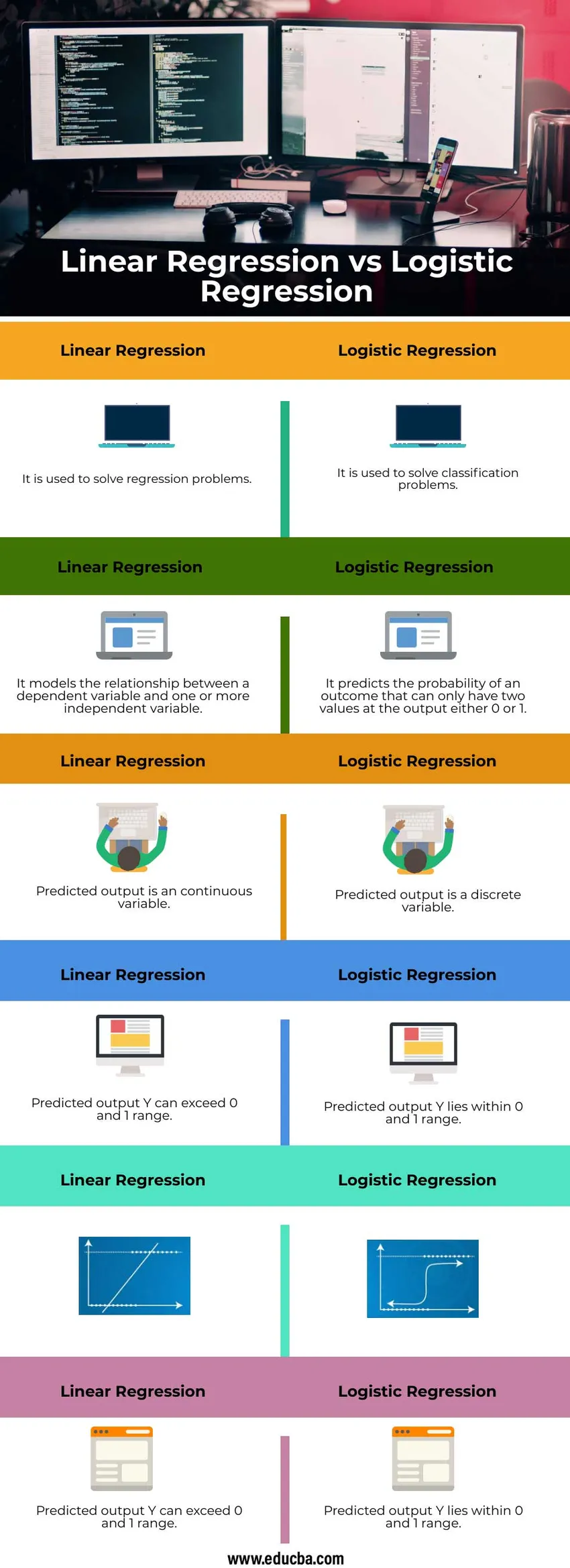
Klíčový rozdíl mezi lineární regresí vs. logistickou regresí
Pojďme diskutovat o některých hlavních klíčových rozdílech mezi lineární regresí a logistickou regresí
Lineární regrese
- Je to lineární přístup
- Používá přímku
- Nemůže brát kategorické proměnné
- Musí ignorovat pozorování s chybějícími hodnotami číselné nezávislé proměnné
- Výstup Y je uveden jako
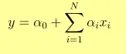
- 1 jednotka zvýšení x zvyšuje Y o α
Aplikace
- Předpovídání ceny produktu
- Predikce skóre v zápase
Logistická regrese
- Je to statistický přístup
- Používá sigmoidní funkci
- Může mít kategorické proměnné
- Může přijímat rozhodnutí, i když jsou přítomna pozorování s chybějícími hodnotami
- Výstup Y je uveden jako, kde z je uveden jako
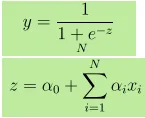
- 1 jednotka zvýšení x zvyšuje Y o log kurzy α
- Jestliže P je pravděpodobnost události, pak (1-P) je pravděpodobnost, že k ní nedojde. Kurzy úspěchu = P / 1-P
Aplikace
- Předpovídání, zda dnes prší nebo ne.
- Předpovídání, zda je e-mail spamem nebo ne.
Srovnávací tabulka lineární regrese vs. logistické regrese
Pojďme diskutovat o nejlepším srovnání mezi lineární regresí proti logistické regresi
|
Lineární regrese |
Logistická regrese |
| Používá se k řešení regresních problémů | Používá se k řešení klasifikačních problémů |
| Modeluje vztah mezi závislou proměnnou a jednou nebo více nezávislými proměnnými | Předpovídá pravděpodobnost výsledku, který může mít na výstupu pouze dvě hodnoty buď 0 nebo 1 |
| Předpovídaný výstup je spojitá proměnná | Předpovídaný výstup je diskrétní proměnná |
| Předpokládaný výstup Y může přesáhnout rozsah 0 a 1 | Předpokládaný výstup Y leží v rozsahu 0 a 1 |
 | 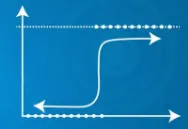 |
| Předpokládaný výstup Y může přesáhnout rozsah 0 a 1 | Předvídaný výstup |
Závěr
Pokud funkce nepřispívají k predikci nebo pokud jsou do velké míry ve vzájemném vztahu, přidá modelu šum. Proto musí být odstraněny funkce, které dostatečně nepřispívají k modelu. Pokud jsou nezávislé proměnné vysoce korelovány, může to způsobit problém vícenásobnosti, který lze vyřešit spuštěním samostatných modelů s každou nezávislou proměnnou.
Doporučené články
Toto byl průvodce po lineární regrese vs. logistické regrese. Zde diskutujeme klíčové rozdíly lineární regrese vs. logistické regrese s infografikou a srovnávací tabulkou. Další informace naleznete také v následujících článcích -
- Data Science vs Vizualizace dat
- Strojové učení vs neuronová síť
- Dozorované učení vs Hluboké učení
- Logistická regrese v R