
Úvod do DFS algoritmu
DFS je známý jako algoritmus hloubky prvního vyhledávání, který poskytuje kroky k procházení každého uzlu grafu bez opakování jakéhokoli uzlu. Tento algoritmus je stejný jako hloubka prvního traversalu pro strom, ale liší se v udržování booleovské hodnoty, aby zkontroloval, zda již byl uzel navštíven nebo ne. To je důležité pro průchod grafu, protože v grafu také existují cykly. V tomto algoritmu je udržován zásobník, který ukládá zavěšené uzly během průchodu. Jmenuje se to proto, že nejprve cestujeme do hloubky každého sousedního uzlu a pak pokračujeme v procházení dalším sousedním uzlem.
Vysvětlete algoritmus DFS
Tento algoritmus je v rozporu s algoritmem BFS, kde jsou navštěvovány všechny sousední uzly, za nimiž následují sousedé sousedních uzlů. Začne zkoumat graf z jednoho uzlu a prozkoumá jeho hloubku před zpětným sledováním. V tomto algoritmu jsou zvažovány dvě věci:
- Návštěva vrcholu: Výběr vrcholu nebo uzlu grafu, který má procházet.
- Průzkum vrcholu: Procházení všemi uzly sousedícími s tímto vrcholem.
Pseudo kód pro první hloubku hledání :
proc DFS_implement(G, v):
let St be a stack
St.push(v)
while St has elements
v = St.pop()
if v is not labeled as visited:
label v as visited
for all edge v to w in G.adjacentEdges(v) do
St.push(w)
Lineární Traversal existuje také pro DFS, který lze implementovat 3 způsoby:
- Předobjednávka
- V pořádku
- PostOrder
Reverzní postorder je velmi užitečný způsob, jak procházet a používat při topologickém třídění a různých analýzách. Zásobník je také udržován pro uložení uzlů, jejichž průzkum stále čeká.
Posouvání grafu v DFS
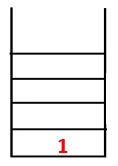
V DFS se postupuje podle níže uvedených kroků k procházení grafu. Například daný graf, začněme přechod od 1:
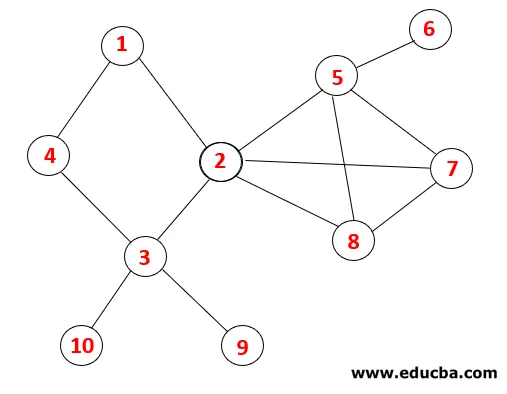
| Zásobník | Traversal Sequence | Spanning Tree |
| 1 |  |
|
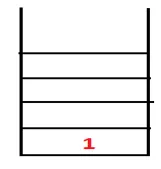 | 1, 4 |  |
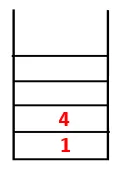 | 1, 4, 3 |  |
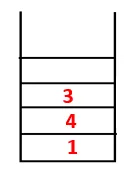 | 1, 4, 3, 10 | 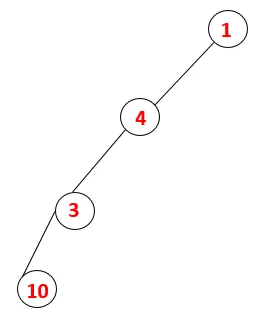 |
 | 1, 4, 3, 10, 9 | 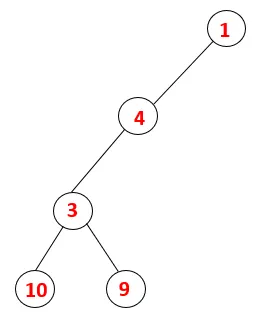 |
 | 1, 4, 3, 10, 9, 2 | 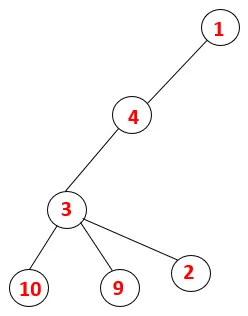 |
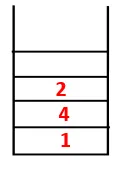 | 1, 4, 3, 10, 9, 2, 8 |  |
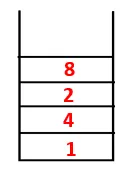 | 1, 4, 3, 10, 9, 2, 8, 7 | 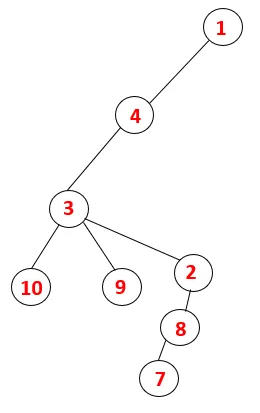 |
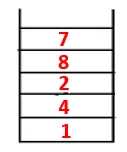 | 1, 4, 3, 10, 9, 2, 8, 7, 5 |  |
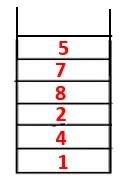 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 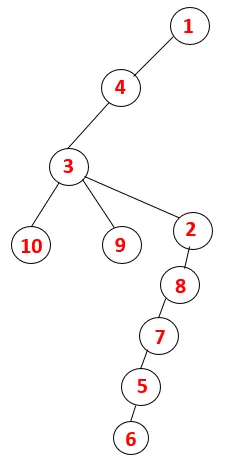 |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 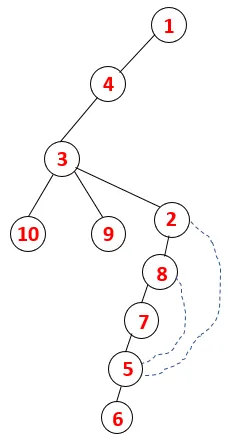 |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 |  |
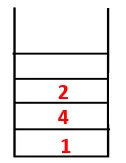 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 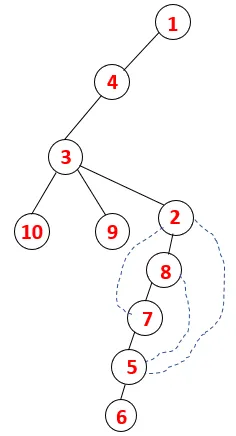 |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 |  |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 |  |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 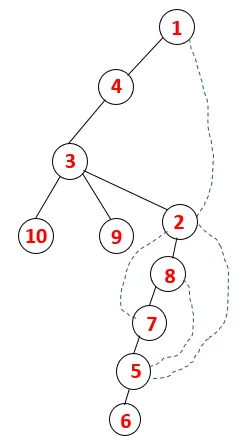 |
Vysvětlení algoritmu DFS
Níže jsou uvedeny kroky k algoritmu DFS s výhodami a nevýhodami:
Krok 1 : Uzel 1 je navštíven a přidán do sekvence i do překlenovacího stromu.
Krok 2: Prozkoumají se sousední uzly 1, což je 4, takže 1 se posune do zásobníku a 4 se posune do sekvence i do překlenovacího stromu.
Krok 3: Prozkoumá se jeden ze sousedních uzlů 4, a tak se 4 posune do zásobníku a 3 vstoupí do posloupnosti a překlenovacího stromu.
Krok 4: Sousední uzly 3 jsou prozkoumány jejich zatlačením do zásobníku a 10 vstupuje do sekvence. Protože neexistuje žádný přilehlý uzel k 10, tak se 3 vyskočí ze zásobníku.
Krok 5: Prozkoumá se další sousední uzel 3 a 3 se zatlačí do zásobníku a navštíví se 9. Žádný sousední uzel 9, tedy 3, není vysunut a je navštíven poslední sousední uzel 3, tj. 2.
Podobný proces je sledován pro všechny uzly, dokud se zásobník nevyprázdní, což indikuje stav zastavení pro algoritmus procházení. - -> tečkované čáry v překlenovacím stromu se vztahují k zadním okrajům v grafu.
Tímto způsobem se všechny uzly v grafu posouvají bez opakování některého z uzlů.
Výhody a nevýhody
- Výhody: Tento požadavek na paměť pro tento algoritmus je velmi menší. Menší složitost prostoru a času než BFS.
- Nevýhody: Řešení není zaručeno Aplikace. Topologické třídění. Hledání mostů grafu.
Příklad implementace algoritmu DFS
Níže je uveden příklad implementace algoritmu DFS:
Kód:
import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)
Výstup:
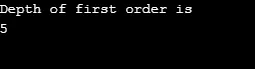
Vysvětlení k výše uvedenému programu: Vytvořili jsme graf s 5 vrcholy (0, 1, 2, 3, 4) a pomocí navštíveného pole sledovali všechny navštívené vrcholy. Potom pro každý uzel, jehož sousední uzly existují, se stejný algoritmus opakuje, dokud se nenavštíví všechny uzly. Potom se algoritmus vrátí zpět k volání vrcholu a vyskočí ze zásobníku.
Závěr
Paměťová náročnost tohoto grafu je ve srovnání s BFS menší, protože je třeba udržovat pouze jeden zásobník. Výsledkem je vygenerovaný spanningový strom DFS a sekvence procházení, ale není konstantní. V závislosti na počátečním vrcholu a zvoleném vrcholu průzkumu je možné více posloupností procházení.
Doporučené články
Toto je průvodce algoritmem DFS. Zde diskutujeme postupné vysvětlení, procházíme grafem v tabulkovém formátu s výhodami a nevýhodami. Další informace naleznete také v dalších souvisejících článcích -
- Co je to HDFS?
- Algoritmy hlubokého učení
- Příkazy HDFS
- Algoritmus SHA