Co je to algoritmus SVM?
SVM je zkratka pro Support Vector Machine. SVM je algoritmus strojového učení pod dohledem, který se běžně používá pro klasifikaci a regresní výzvy. Mezi běžné aplikace algoritmu SVM patří systém detekce narušení, rozpoznávání rukopisu, predikce struktury proteinů, detekce steganografie v digitálních obrazech atd.
V algoritmu SVM je každý bod reprezentován jako datová položka v n-dimenzionálním prostoru, kde hodnota každého prvku je hodnota konkrétní souřadnice.
Po vykreslení byla klasifikace provedena nalezením roviny hype, která rozlišuje dvě třídy. Pro pochopení této koncepce viz obrázek níže.
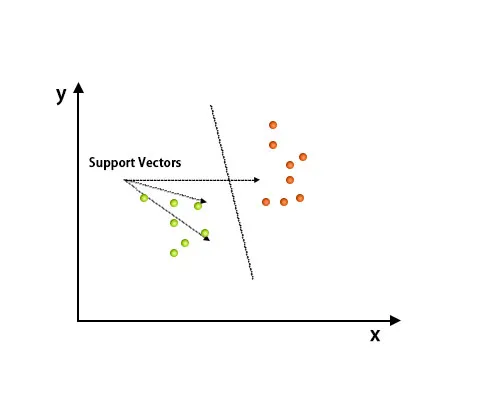
Algoritmus Support Vector Machine se používá hlavně k řešení klasifikačních problémů. Podpůrné vektory nejsou nic jiného než souřadnice každé datové položky. Support Vector Machine je hranice, která rozlišuje dvě třídy pomocí hyper-letadla.
Jak funguje algoritmus SVM?
Ve výše uvedené části jsme diskutovali o diferenciaci dvou tříd pomocí hyper-roviny. Nyní se podíváme, jak tento algoritmus SVM skutečně funguje.
Scénář 1: Určete pravou hyperrovinu
Zde jsme vzali tři hyper-roviny, tj. A, B a C. Nyní musíme určit pravou hyper-rovinu pro klasifikaci hvězdy a kruhu.
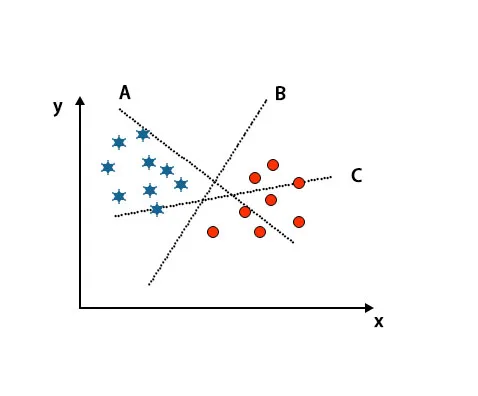
Abychom určili správnou hyper-rovinu, měli bychom znát palcové pravidlo. Vyberte hyper rovinu, která rozlišuje dvě třídy. Na výše uvedeném obrázku hyper-rovina B velmi dobře rozlišuje dvě třídy.
Scénář 2: Určete pravou hyperrovinu
Zde jsme vzali tři hyperplochy, tj. A, B a C. Tyto tři hyperplochy již velmi dobře rozlišují třídy.
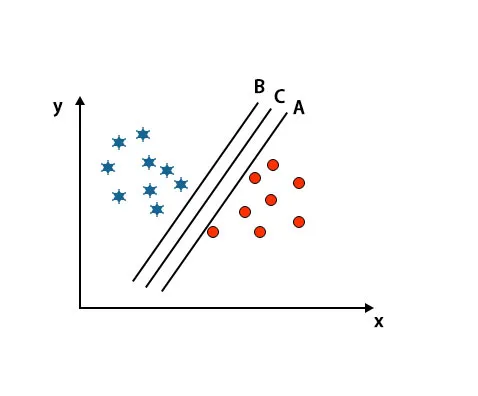
V tomto scénáři pro identifikaci správné hyper roviny zvětšujeme vzdálenost mezi nejbližšími datovými body. Tato vzdálenost není nic jiného než okraj. Viz obrázek níže.
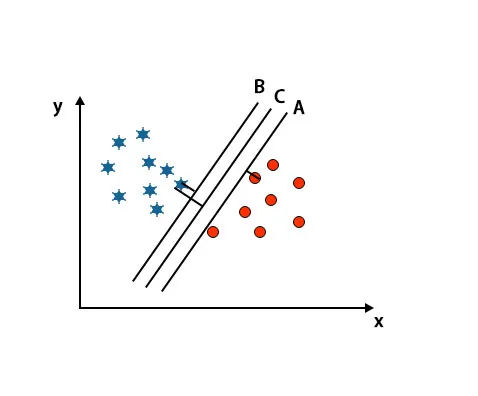
Na výše uvedeném obrázku je okraj hyper-roviny C vyšší než hyper-rovina A a hyper-rovina B. Takže v tomto scénáři je C pravá hyper rovina. Pokud zvolíme hyperplán s minimálním rozpětím, může to vést k nesprávné klasifikaci. Proto jsme si vybrali hyperplán C s maximálním rozpětím kvůli robustnosti.
Scénář 3: Určete pravou hyperrovinu
Poznámka: Pro identifikaci hyper-roviny postupujte podle stejných pravidel jako v předchozích oddílech.
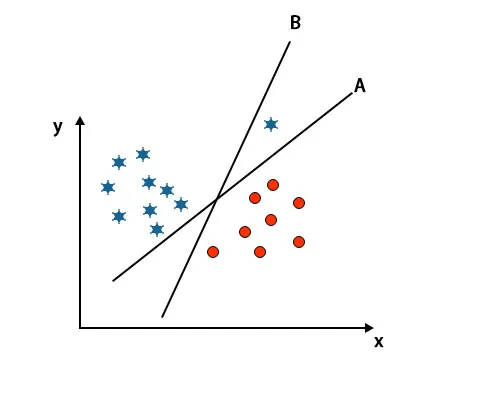
Jak vidíte na výše uvedeném obrázku, okraj hyper-roviny B je vyšší než okraj hyper-roviny A, proto někteří vyberou hyper-rovinu B jako právo. Ale v algoritmu SVM vybere tuto hyper-rovinu, která klasifikuje třídy přesné před maximalizací marže. V tomto scénáři hyper-rovina A klasifikovala všechny přesně a existuje určitá chyba s klasifikací hyper-roviny B. Proto A je pravá hyper-rovina.
Scénář 4: Klasifikujte dvě třídy
Jak vidíte na níže uvedeném obrázku, nedokážeme rozlišit dvě třídy pomocí přímky, protože jedna hvězda leží jako odlehlé místo v jiné kruhové třídě.
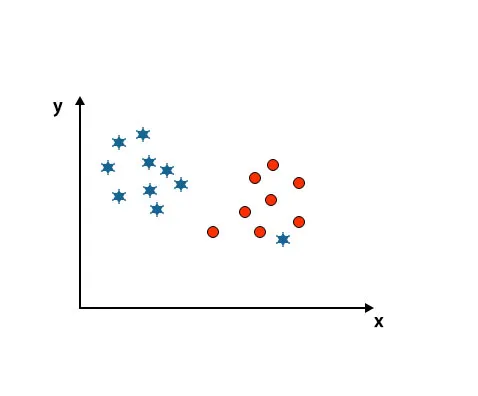
Jedna hvězda je zde v jiné třídě. Pro třídu hvězd je tato hvězda odlehlou. Vzhledem k robustnosti vlastnosti algoritmu SVM najde pravou hyperplánu s vyšším okrajem ignorující odlehlé hodnoty.
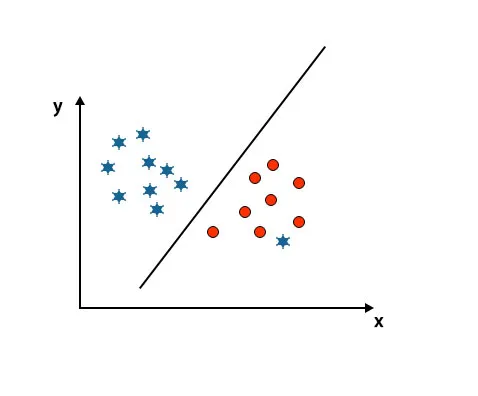
Scénář 5: Jemná hyper-rovina pro rozlišení tříd
Doposud jsme se dívali na lineární hyper-rovinu. Na níže uvedeném obrázku nemáme mezi třídami lineární hyper rovinu.
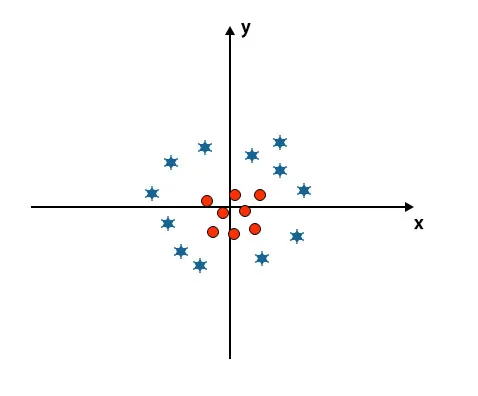
Pro klasifikaci těchto tříd SVM zavádí některé další funkce. V tomto scénáři použijeme tuto novou funkci z = x 2 + y 2.
Vykreslí všechny datové body na ose x a z.

Poznámka
- Všechny hodnoty na ose z by měly být kladné, protože z se rovná součtu x na druhou a na druhou na druhou.
- Ve výše uvedeném grafu jsou červené kruhy uzavřeny k počátku osy x a osy y, což vede k tomu, že hodnota z je nižší a hvězda je přesně opačná kružnice, je od počátku osy x a osa y, což vede k hodnotě z.
V algoritmu SVM je snadné klasifikovat pomocí lineární hyperplane mezi dvěma třídami. Zde však vyvstává otázka, měli bychom přidat tuto funkci SVM k identifikaci hyper-roviny. Odpověď tedy zní ne, k vyřešení tohoto problému má SVM techniku, která je běžně známá jako trik jádra.
Trik jádra je funkce, která transformuje data do vhodné formy. V algoritmu SVM se používají různé typy funkcí jádra, např. Polynomiální, lineární, nelineární, funkce radiálního základu atd. Zde se pomocí jaderného triku převádí nízkodimenzionální vstupní prostor na prostorový prostor.
Když se podíváme na hyperplošinu počátek osy a osy y, vypadá to jako kruh. Viz obrázek níže.
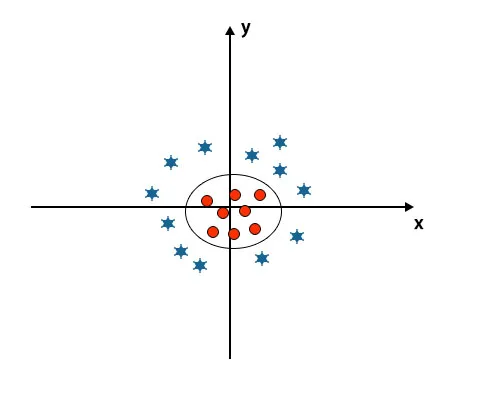
Výhody SVM algoritmu
- I když jsou vstupní data nelineární a neoddělitelná, generují SVM díky své robustnosti přesné výsledky klasifikace.
- Ve rozhodovací funkci používá podskupinu tréninkových bodů nazývaných podpůrné vektory, takže je efektivní z paměti.
- Je vhodné vyřešit jakýkoli složitý problém vhodnou funkcí jádra.
- V praxi jsou modely SVM zobecněny, s menším rizikem nadměrného osazení v SVM.
- SVM funguje skvěle pro klasifikaci textu a při hledání nejlepšího lineárního oddělovače.
Nevýhody algoritmu SVM
- Při práci s rozsáhlými datovými soubory trvá dlouhou dobu školení.
- Je těžké pochopit konečný model a individuální dopad.
Závěr
Byla vedena podpora algoritmu Vector Machine Algorithm, což je algoritmus strojového učení. V tomto článku jsme diskutovali, co je algoritmus SVM, jak to funguje a jaké jsou jeho výhody.
Doporučené články
Toto byl průvodce algoritmem SVM. Zde diskutujeme o jeho práci se scénářem, výhodami a nevýhodami algoritmu SVM. Další informace naleznete také v následujících článcích -
- Algoritmy dolování dat
- Techniky dolování dat
- Co je strojové učení?
- Nástroje strojového učení
- Příklady algoritmu C ++