
Úvod do příkladů standardní odchylky
Existuje mnoho příkladů standardních odchylek. Standardní odchylka je míra rozptylu datového souboru, tj. Jak jsou rozprostřena čísla. Je užitečné pro porovnání různých sad dat, které by mohly mít stejný průměr, ale různý rozsah. Následující příklad standardní směrodatné odchylky poskytuje porozumění nejběžnějším typům situací, kdy se směrodatná odchylka počítá a jak lze vypočítat stejnou odchylku.
Příklady standardní odchylky
Níže jsou uvedeny příklady standardní odchylky
Standardní odchylka - Příklad č. 1
Akcie společnosti Z prodávají za 50 USD za akcii a stejné nabídky nabízejí následující výplaty pro příští rok:
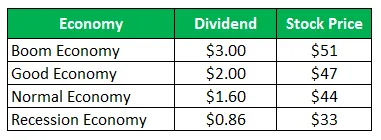
Vypočítejte směrodatnou odchylku, pokud jsou všechny čtyři scénáře stejně pravděpodobné.
Řešení:
Výpočty doby uchování období (HPR) jsou následující -
Vzorec HPR
HPR = ((hodnota na konci období - původní hodnota) + příjem) / původní hodnota) * 100
Pro Boom Economy
- HPR (Boom) = ((51-50) + 3) / 50 = 8, 00%
- HPR (Dobrý) = ((47-50) + 2) / 50 = -2, 00%
- HPR (normální) = ((44-50) + 1, 60) / 50 = -8, 80%
- HPR (Recese) = ((33-50) + 0, 86) / 50 = -32, 28%
Výpočet očekávaného výnosu
Protože všechny scénáře jsou stejně pravděpodobné, pravděpodobnost všech bude ¼
Vzorec očekávaného návratu
Očekávaný návrat = (Pravděpodobnost rozmachu * Návrat z rozmachu) + (Pravděpodobnost dobrého * Návrat z dobrého) + (Pravděpodobnost normálu * Návrat z normálu) + (Pravděpodobnost recese * Návrat z recese)
- Očekávaný výnos = (1/4 x 8%) + (1/4 x -2%) + (1/4 x -8, 80%) + (1/4 x -32, 28%)
- Očekávaný výnos = -8, 77%
Výpočet směrodatné odchylky
Vzorec variace
Variance = (Pravděpodobnost rozmachu * (Návrat z rozmachu - celkový očekávaný výnos) 2) + (Pravděpodobnost dobrého * (návratnost z dobrého - celkový očekávaný výnos) 2) + (Pravděpodobnost normálu * (Návrat z normálu - celkový očekávaný výnos) 2 ) + (Pravděpodobnost recese * (návrat z recese - celkový očekávaný návrat) 2)
- Varianta = 1/4 (8 - (-8, 77)) 2 + 1/4 (-2 - (-8, 77)) 2 + 1/4 (-8, 80 - (-8, 77)) 2 + 1/4 (-32, 28 - (-8, 77)) 2
- Varianta = 219, 95
Vzorec standardní odchylky
Standardní odchylka bude druhá odmocnina
Standard Deviation = √Viance
- Standardní odchylka = √ 219, 95
- Standardní odchylka = 14, 83%
Příklad standardní odchylky - 2
Standardní odchylka v případě dvou společností v portfoliu
Kmenové akcie společnosti A prodávají za 28 USD za akcii a stejné nabídky po výplatách pro příští rok

Kmenové akcie společnosti B prodávají za 93 USD za akcii a stejné nabídky nabízejí následující výplaty pro příští rok:

(a) Vypočítejte směrodatnou odchylku společnosti A
(b) Vypočítejte směrodatnou odchylku společnosti B
(c) Vypočítat směrodatnou odchylku portfolia, pokud je provedena polovina investice, je společnost A a zbytek polovina ve společnosti B
Řešení:
Pro společnost A
Výpočty návratnosti doby uchování (HPR)
Vzorec HPR
HPR = ((hodnota na konci období - původní hodnota) + příjem) / původní hodnota) * 100
- HPR (boom) = ((20-28) + 1) / 28 = -25, 00%
- HPR (normální) = ((30-28) + 1, 50 / 28 = 12, 50%
- HPR (Recese) = ((38-28) + 5) / 28 = 53, 57%
Výpočet očekávaného návratu společnosti A
Vzorec očekávaného návratu
Očekávaný návrat = (Pravděpodobnost rozmachu * Návrat z rozmachu) + (Pravděpodobnost normálu * Návrat z normálu) + (Pravděpodobnost recese * Návrat z recese)
- Očekávaný výnos = (0, 45 x -25, 00%) + (0, 35 x 12, 50%) + (0, 20 x 53, 57%)
- Očekávaný výnos = 3, 84%
Výpočet společnosti se standardní odchylkou A
Vzorec variace
Variance = (Pravděpodobnost rozmachu * (Návrat z rozmachu - celkový očekávaný výnos) 2) + (Pravděpodobnost normálu * (Návrat z normálu - celkový očekávaný výnos) 2 ) + (Pravděpodobnost recese * (Návrat z recese - Celkový očekávaný výnos) 2)
- Varianta = 0, 45 (-25, 00 - (3, 84)) 2 + 0, 35 (12, 50 - (3, 84)) 2 + 0, 20 (53, 57 - (3, 84)) 2
- Varianta = 895, 15
Vzorec standardní odchylky
Standardní odchylka bude druhá odmocnina
Standard Deviation = √Viance
- Standardní odchylka = √ 895, 15
- Standardní odchylka = 29, 92%
Pro společnost B
Výpočty návratnosti doby uchování (HPR)
Vzorec HPR
HPR = ((hodnota na konci období - původní hodnota) + příjem) / původní hodnota) * 100
HPR (Boom) = ((200-93) +7) / 93 = 122, 58%
HPR (normální) = ((105-93) + 5, 50 / 93 = 18, 82%
HPR (Recese) = ((4-93) +2) / 93 = -93, 55%
Výpočet očekávaného výnosu
Vzorec očekávaného návratu
Očekávaný návrat = (Pravděpodobnost rozmachu * Návrat z rozmachu) + (Pravděpodobnost normálu * Návrat z normálu) + (Pravděpodobnost recese * Návrat z recese)
- Očekávaný výnos = (0, 45 x 122, 58%) + (0, 35 x 18, 82%) + (0, 20 x -93, 55%)
- Očekávaný výnos = 43, 04%
Výpočet směrodatné odchylky
Vzorec variace
Variance = (Pravděpodobnost rozmachu * (Návrat z rozmachu - celkový očekávaný výnos) 2) + (Pravděpodobnost normálu * (Návrat z normálu - celkový očekávaný výnos) 2 ) + (Pravděpodobnost recese * (Návrat z recese - Celkový očekávaný výnos) 2)
- Varianta = 0, 45 (122, 58– (43, 04)) 2 + 0, 35 (18, 82– (43, 04)) 2 + 0, 20 (-93, 55– (43, 04)) 2
- Varianta = 6783, 65
Vzorec standardní odchylky
Standardní odchylka bude druhá odmocnina
Standard Deviation = √Viance
- Standardní odchylka = 6783, 65
- Standardní odchylka = 82, 36%
Výpočet očekávaného výnosu a směrodatné odchylky portfolia poloviny investované do společnosti A a poloviny do společnosti B.
Standardní odchylka společnosti A = 29, 92%
Standardní odchylka společnosti B = 82, 36%
Hmotnost společnosti A = 0, 50
Hmotnost společnosti B = 0, 50
Vzorec standardní odchylky portfolia
Standardní odchylka portfolia = (váha společnosti A * očekávaná návratnost společnosti A) + ((váha společnosti B * očekávaná návratnost společnosti B)
- Standardní odchylka portfolia = (0, 50 * 29, 92) + (0, 50 * 82, 36)
- Standardní odchylka portfolia = 56, 14%
Analýza
Směrodatná odchylka portfolia je nižší než u jednotlivců jednotlivých akcií, protože akcie jsou diverzifikovány do různých akcií. Diverzifikace vede ke snížení rizika, pokud neexistuje dokonalá korelace mezi návratností portfoliových investic.
Závěr - příklady standardní odchylky
Standardní odchylka měří rozptyl datového souboru, který je relativní k jeho střední hodnotě. Vypočítá se jako druhá odmocnina rozptylu. Čím větší je standardní odchylka cenného papíru, tím větší bude rozptyl mezi každou cenou a průměrem, což ukazuje, že cenové rozpětí je velké. Výše uvedené příklady jsou některé z příkladů standardní odchylky různými způsoby. Existují také různé další příklady, které ukazují, že směrodatná odchylka může být vypočtena pomocí jiných dat.
Doporučené články
Toto byl průvodce standardními příklady odchylek. Zde diskutujeme různé příklady standardní odchylky spolu s podrobným vysvětlením . Další informace naleznete také v následujících článcích -
- Příklad fixních nákladů
- Příklad variabilní kalkulace
- Příklad kvantitativního výzkumu
- Příklady monopolistické soutěže