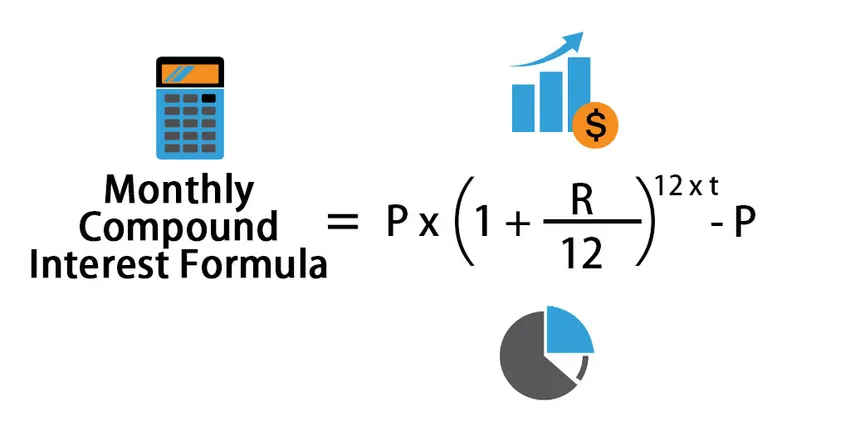
Měsíční složený úrokový vzorec Příklady se šablonou Excel

Měsíční složený úrokový vzorec (obsah)

• Vzorec
• Příklady
• Kalkulačka

Co je měsíční složený úrokový vzorec?

Je-li určité množství peněz vypůjčeno na konkrétní dobu a navíc se musí vypůjčit navíc spolu s vypůjčenou částkou. Pak se dodatečná částka, kterou platíme pevnou sazbou, nazývá úroky. Složený úrok je celkový úrok, který zahrnuje původní úrok a úrok nové jistiny, který se vyvinul přidáním původní jistiny k splatnému úroku. Pro výpočet měsíčního úroku je úrok, který je složen celý měsíc po celý rok.

Měsíční složený úrokový vzorec lze vypočítat jako:

Monthly Compound Interest Formula = P * (1 + (R /12)) 12*t – P

kde,

• P = hlavní částka
• R = míra
• t = čas

Příklady vzorce měsíčního úrokového úroku (se šablonou Excel)

Vezměme si příklad, abychom lépe porozuměli výpočtu měsíčního úrokového úroku.

Tuto šablonu měsíčního složeného úrokového vzorce si můžete stáhnout zde - šablonu měsíčního složeného úrokového vzorce Excel

Vzorec úroků za měsíc - příklad # 1

Dlužník si půjčil částku 10 000 Rs sazbou 8%. Vypočítat měsíční složenou úrokovou sazbu na 2 roky?

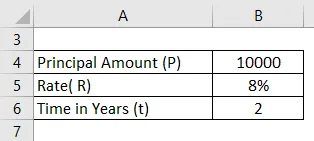
Řešení:

Měsíční úrokový úrok se vypočítá pomocí vzorce uvedeného níže

Měsíční úrokový úrok = P * (1 + (R / 12)) ^{12 * t} - P

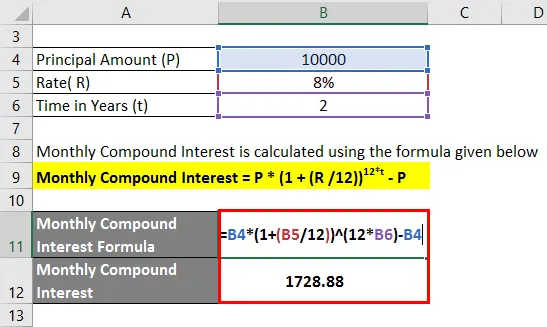
• Měsíční úrokový úrok = 10 000 (1 + (8/12)) ^{2 * 12} - 10 000
• Měsíční složený úrok = 1 728, 88

Měsíční složený úrok po dobu 2 let je R 1 728, 88

Vzorec úroků za měsíc - příklad # 2

Částka peněz je investována ve výši 10% je 20 000 Rs. Jaký bude měsíční složený úrok za 10 let?

Řešení:

Měsíční úrokový úrok se vypočítá pomocí vzorce uvedeného níže

Měsíční úrokový úrok = P * (1 + (R / 12)) ^{12 * t} - P

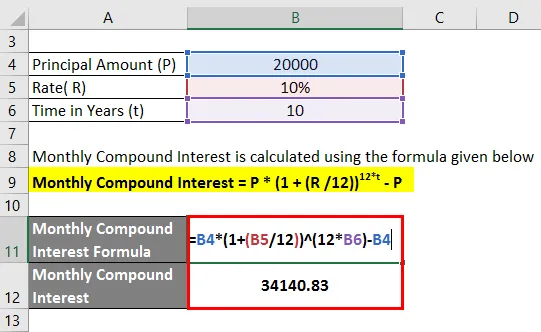
• Měsíční úrokový úrok = 20 000 (1 + 10/12)) ^{10 * 12} - 20 000
• Měsíční složený úrok = 34, 140, 83

Měsíční složený úrok po dobu 10 let je R 34, 140, 83

Vzorec úrokových sazeb za měsíc - Příklad č. 3

Paní Jeffersonová koupila starožitný status za 500 dolarů. O pět let později tento stav prodala za 800 dolarů. Považovala to za součást investice. Vypočítat roční sazbu, kterou získala?

Řešení:

Pokud vezmeme v úvahu investici 500 USD a získáme 800 USD v budoucím časovém úseku po t = 10 letech. Předpokládáme roční sazbu m = 1 a implementujeme ji do vzorce.

A = P (1 + r / m) ^mt

• 800 = 500 (1+ r / 1) ^{1 x 10}
• 800 = 500 (1 + r) ¹⁰

Nyní řešíme sazbu (r) v následujících krocích.

• 800 = 500 (1 + r) ¹⁰
• 8/5 = (1 + r) ¹⁰

Nyní vezmeme sílu (1/10) na levé straně rovnice a vyjasníme z pravé strany.

• (8/5) ^1/10) = 1 + r

Vypočítejte hodnotu vlevo a vyřešte pro r.

• 1, 0481 = 1 + r
• 1, 0481 - 1 = r
• 0, 0481 = r

Paní Jeffersonová však dosáhla roční úrokové sazby 4, 81%, což není špatná míra návratnosti.

Vysvětlení

Složené úroky jsou součtem počáteční částky jistiny o jednu plus roční úroková sazba zvýšená na počet složených období minus jeden. Počáteční částka půjčky se odečte od výsledné hodnoty.

Složený úrok lze vypočítat jako:

Vzorec úrokového vzorce = (P (1 + i) ⁿ ) - P

Složená úroková rovnice = (P (1 + i) ⁿ - 1)

Kde:

• P = hlavní částka
• i = roční úroková sazba v procentech
• n = období smíchání

Existuje určitá sada postupů, pomocí kterých můžeme vypočítat Měsíční složený úrok.

Krok 1: Musíme vypočítat výši úroku získaného pomocí měsíčního úrokového úroku. Vzorec lze vypočítat jako:

• A = (P (1 + i) ⁿ - 1) - P

Krok 2: pokud předpokládáme, že úroková sazba je 5% ročně. Nejprve musíme vyjádřit úrokovou hodnotu do ekvivalentního desetinného čísla. To lze provést následujícím způsobem.

• 5% = 5/100 = 0, 05

Krok 3: Protože víme, že úrok je složen měsíčně, takže můžeme vzít n = 12. Časové období je však v tomto případě stanoveno, ale uvažujeme, že půjčka je přijata na dobu jednoho roku. Nyní máme k dispozici všechny proměnné, které můžeme přímo nahradit do vzorce a získat z něj výsledek.

• A = 1000 ((1 + 0, 05 / 12) ¹² - 1)
• A = 1000 ((1 + 0, 0042) ¹² - 1)
• A = 1000 ((1, 0042) ¹² - 1)
• A = 1 000 (1, 0516 - 1)
• A = 1 000 (0, 0516)
• A = 51, 6

Vypočítali jsme úrokovou sazbu na 1 rok měsíčním složením jako asi 51, 6

Měsíční složené úroky neodrážejí znatelné změny, pokud zaparkujeme určité množství peněz na krátkou dobu. Důvodem je to, že sloučení trvá několik let, než se projeví znatelné změny.

A nejvýznamnější věc o složeném úroku je, že vaše investice rostou rychleji než jednoduchý úrok. Čím častěji je váš kombinovaný interval, tím větší je rozdíl, nebo můžeme říci, že denní úrokový úrok vytváří vyšší příjem z vašich investic než roční složený úrok pro danou úrokovou sazbu.

Následující tabulka ukazuje rozdíl, že počet kombinovaných období může během určitého časového období vydělat na půjčku 10 000 $ s roční úrokovou sazbou 10% po dobu 12 let.

Frekvenční složení	Počet období kombinování	Hodnoty pro i a n	Celkový úrok
Každoročně	1	I = 10%, n = 12	21 384, 2837 USD
Pololetně	2	I = 5%, n = 24	22 250, 9999 $
Čtvrtletní	4	I = 2, 5%, n = 48	22 714, 8956 $
Měsíční	12	I = 0, 833%, n = 144	23 036 489 $

Relevance a použití vzorce měsíčního úrokového úroku

Složený úrok se ukázal jako lepší nástroj pro investice, ale může být velmi nebezpečný, pokud je použitelný pro vaši částku půjčky. Nakonec zaplatíte více úroků z vaší půjčky.

Složení se stává účinnějším, pokud je vaše investice buď měsíční, nebo čtvrtletní místo ročně, protože poskytuje lepší návratnost. Pokud si půjčujete peníze od kterékoli banky nebo finanční instituce, je nejlepší volbou roční sloučení. Pokud půjčujete určité množství peněz, bude denní slučování produktivnější. Měli bychom však mít na paměti, že složení může být podle okolností příznivé nebo nepříznivé.

Složené úroky poskytují lepší návratnost investice, záleží na držbě a velikosti investice. Složený úrok roste rychleji, než očekáváte.

Výhody složeného úroku jsou uvedeny níže:

1. Reinvestice
2. Lepší návratnost vaší investice.
3. Dlouhodobé úspory.
4. Zvýšené příjmy.

Měsíční složená úroková kalkulačka

Můžete použít následující měsíční složenou úrokovou kalkulačku

P
R
t
Měsíční složený úrokový vzorec

Měsíční složený úrokový vzorec	P x ((1 + R / 12) 12 * t - P)
=	0 x ((1 +0/12) 12 * 0 - 0) = 0

Doporučené články

Toto je průvodce měsíčním složeným úrokovým vzorcem. Zde diskutujeme, jak vypočítat měsíční složený úrokový vzorec, spolu s praktickými příklady. Poskytujeme také měsíční složenou úrokovou kalkulačku se stahovatelnou šablonou Excel. Další informace naleznete také v následujících článcích -

1. Vzorec pro složenou roční míru růstu
2. Jak vypočítat nominální úrokovou sazbu?
3. Denní složený úrokový vzorec
4. Průvodce Poissonovým distribučním vzorcem
5. Úrok vs dividenda Top 8 klíčových rozdílů, které byste měli vědět