
Úvod do funkcí v R
Funkce je definována jako sada příkazů, které slouží k provedení a provedení jakékoli konkrétní logické úlohy. Funkce bere některé vstupní parametry, které jsou známé jako argumenty k provedení této úlohy. Funkce pomáhají rozbít kód, na jednodušší kousky tím, že jej logicky organizují, což je snáze čitelné a pochopitelné. V tomto tématu se dozvíme o funkcích v R.
Jak psát funkce v R?
Pro zápis funkce v R je zde syntax:
Fun_name <- function (argument) (
Function body
)
Zde je vidět, že v R se používá specifické vyhrazené slovo „funkce“ pro definování jakékoli funkce. Funkce vezme vstup, který je ve formě argumentů. Tělo funkce je sada logických příkazů, které jsou prováděny nad argumenty a poté vrací výstup. „Fun_name“ je jméno dané funkci, prostřednictvím které ji lze volat kdekoli v programu R.
Podívejme se na příklad, který bude přehlednější v chápání pojmu funkce v R.
R kód
Multi <- function(x, y) (
# function to print x multiply y
result <- x*y
print(paste(x, "Multiply", y, "is", result))
)
výstup:
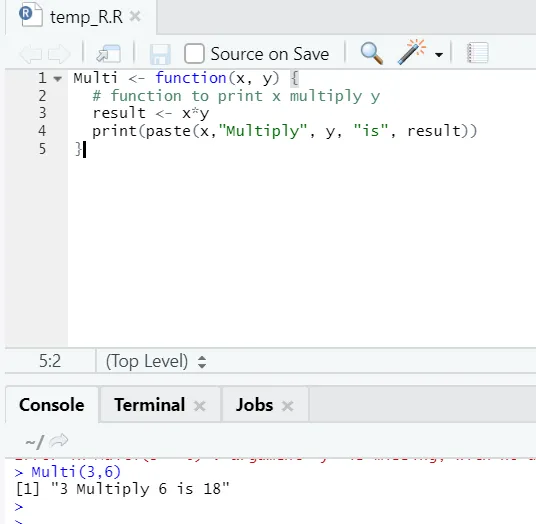
Zde jsme vytvořili název funkce „Multi“, který bere dva argumenty jako vstupy a poskytuje násobený výstup. První argument je x a druhý argument je y. Jak vidíte, funkci jsme nazvali názvem „Multi“. Zde, pokud chce někdo, lze také nastavit výchozí hodnotu argumenty.
Různé typy funkcí v R
Různé funkce R se syntaxí a příklady (vestavěný, matematický, statistický atd.)
1) Vestavěná funkce -
Toto jsou funkce, které přicházejí s R k řešení konkrétního úkolu tím, že berou argument jako vstup a dávají výstup založený na daném vstupu. Pojďme diskutovat o některých důležitých obecných funkcích R zde:
a) Seřadit: Data mohou být seřazena vzestupně nebo sestupně. Data mohou být, zda vektor proměnné pokračuje nebo faktor proměnné.
Syntax:

Zde je vysvětlení jeho parametrů:
- x: Toto je vektor spojité proměnné nebo faktorové proměnné
- klesající: Toto může být nastaveno na True / False pro řízení pořadí vzestupně nebo sestupně. Ve výchozím nastavení je FALSE`.
- last: Pokud má vektor NA hodnoty, měl by být uveden jako poslední nebo ne
R kód a výstup:
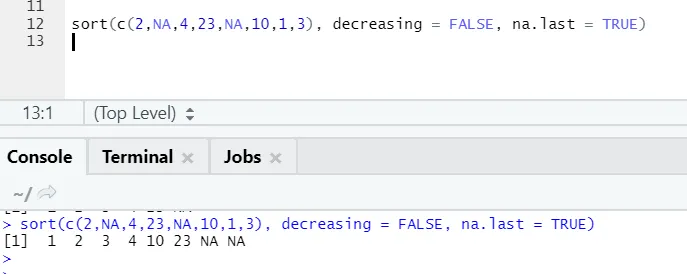
Zde si můžeme všimnout, jak se hodnoty „NA“ na konci vyrovnají. Protože náš parametr na.last = True byl pravdivý.
b) Seq: Generuje posloupnost čísla mezi dvěma zadanými čísly.
Syntax
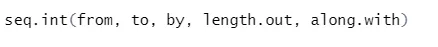
Zde je vysvětlení jeho parametrů:
- od, do počáteční a koncové hodnoty sekvence.
- by: Přírůstek / mezera mezi dvěma po sobě jdoucími čísly v pořadí
- length.out: požadovaná délka sekvence.
- Along.with: Odkazuje na délku od délky tohoto argumentu
R kód a výstup:
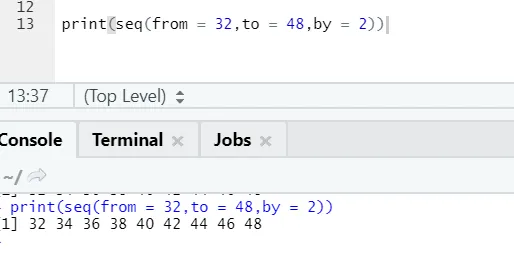
Zde si můžeme všimnout, že vygenerovaná sekvence má přírůstek 2, protože podle je definována jako 2.
c) Toupper, tolower: Dvě funkce: toupper a tolower jsou funkce aplikované na řetězec pro změnu velikosti písmen ve větách.
R kód a výstup:
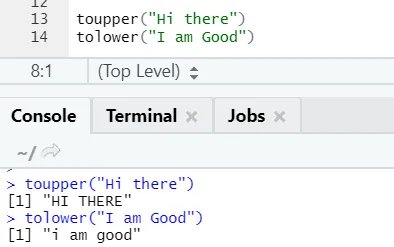
Je možné si všimnout, jak se případy písmen mění při použití funkce.
d) Rnorm: Jedná se o vestavěnou funkci, která generuje náhodná čísla.
R kód a výstup:
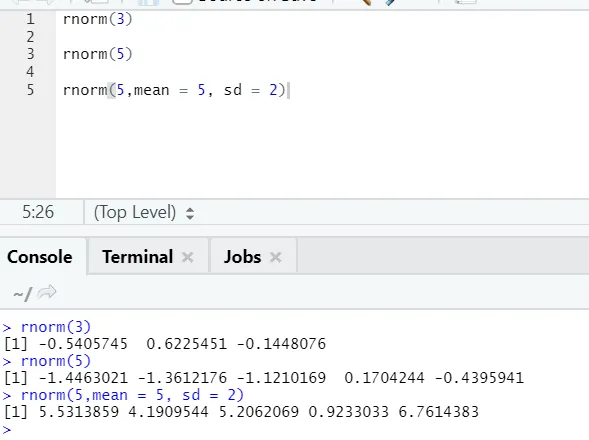
Funkce rnorm vezme první argument, který říká, kolik čísel je třeba vygenerovat.
e) Rep: Tato funkce replikuje hodnotu tolikrát, kolikrát je uvedeno.
Syntaxe R: rnorm (x, n)
Zde x představuje hodnotu pro replikaci a n představuje počet replikací.
R kód a výstup:
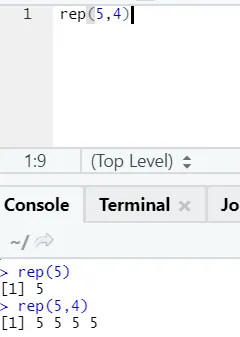
f) Vložit: Tato funkce slouží ke zřetězení řetězců spolu s určitým zvláštním znakem mezi nimi.
syntax
paste(x, sep = “”, collapse = NULL)
R kód
paste("fish", "water", sep=" - ")
R výstup:
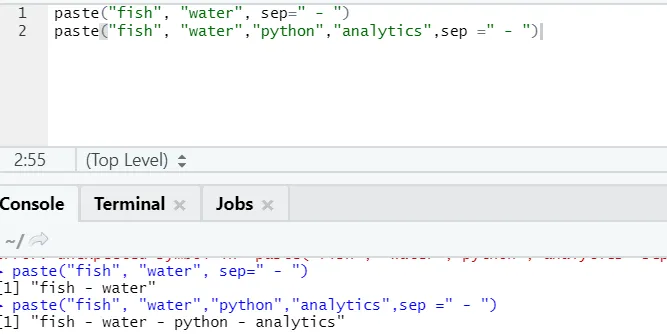
Jak vidíte, můžeme vložit i více než dva řetězce. Sep je ten specifický znak, který jsme přidali mezi řetězce. Ve výchozím nastavení je sep prostor.
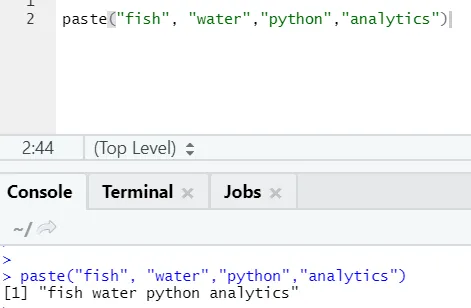
Existuje ještě jedna podobná funkce, jako je tato, kterou by si měli všichni uvědomit, je paste0.
Funkce paste0 (x, y, collapse) funguje podobně jako paste (x, y, sep = “”, collapse)
Viz níže uvedený příklad:
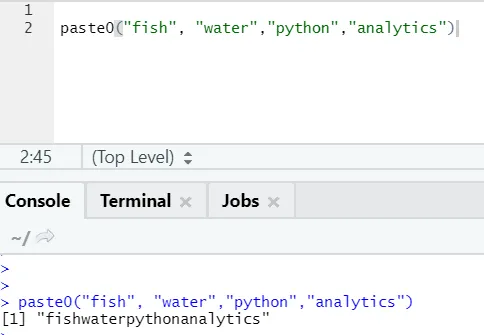
Jednoduše řečeno, shrnout vložit a vložit0:
Paste0 je rychlejší než vložit, pokud jde o zřetězení řetězců bez oddělovače. Jako vložka vždy hledá „sep“, což je ve výchozím nastavení místo.
g) Strsplit: Tato funkce slouží k rozdělení řetězce. Podívejme se na jednoduché případy:
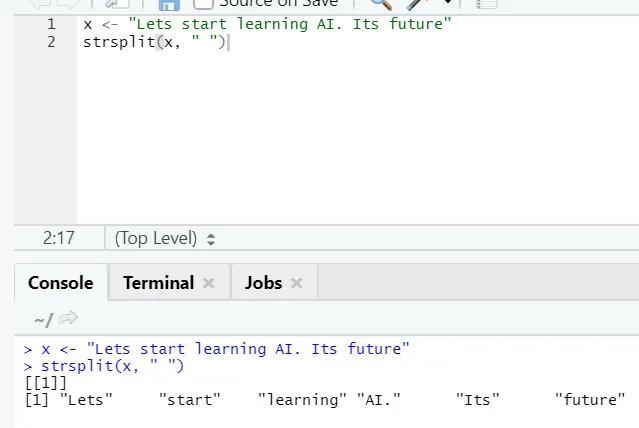
h) Rbind: Funkce rbind pomáhá v česání vektorů se stejným počtem sloupců, jeden nad druhým.
Příklad
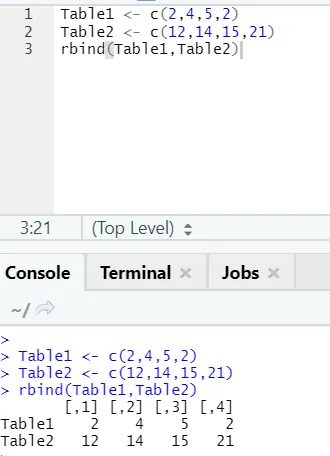
i) cbind: Toto kombinuje vektory se stejným počtem řádků vedle sebe.
Příklad
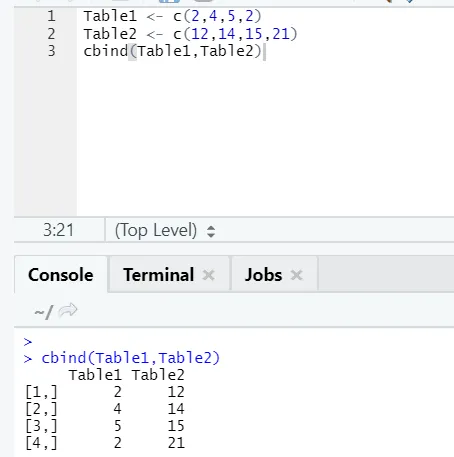
V případě, že se počet řádků neshoduje, najdete níže chybu:

Jak svázat, tak svinout pomáhá při manipulaci s daty a jejich přetvoření.
2) Math Function -
R poskytuje širokou škálu matematických funkcí. Podívejme se na ně několik podrobně:
a) Sqrt: Tato funkce vypočítá druhou odmocninu čísla nebo číselného vektoru.
R kód a výstup:
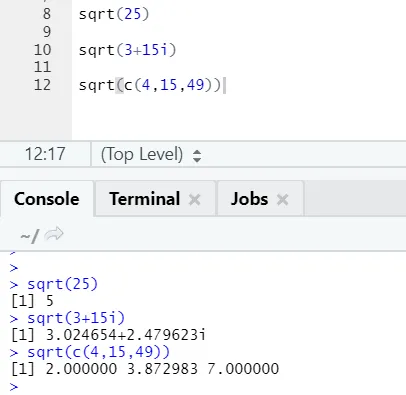
Je vidět, jak se vypočte druhá odmocnina čísla, složité číslo a posloupnost číselného vektoru.
b) Exp: Tato funkce počítá exponenciální hodnotu čísla nebo číselného vektoru.
R kód a výstup:
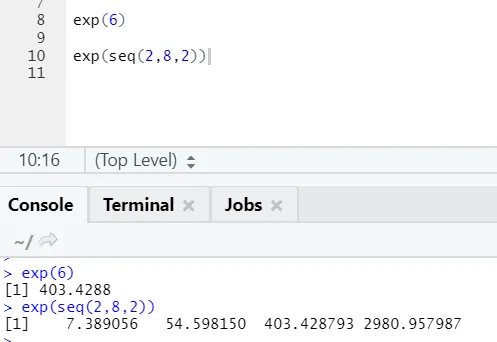
c) Cos, Sin, Tan: Toto jsou trigonometrické funkce implementované v R zde.
R kód a výstup:
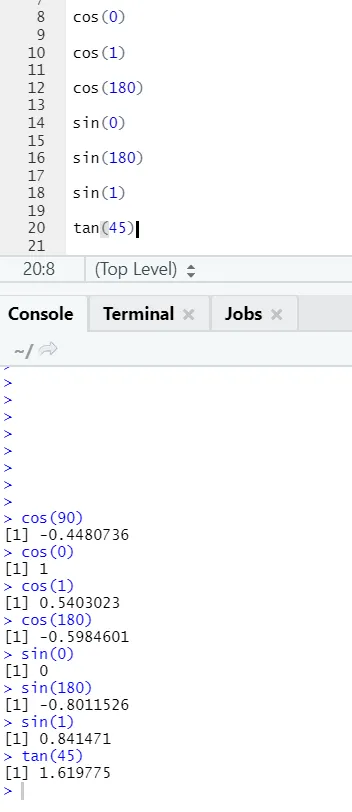
d) Abs: Tato funkce vrací absolutní kladnou hodnotu čísla.
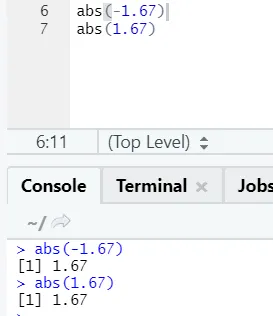
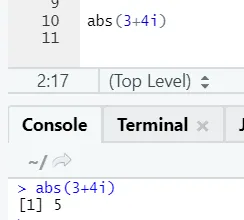
Jak vidíte, záporné nebo kladné číslo bude vráceno v absolutní podobě. Podívejme se na komplexní číslo:
e) Protokol: Zde najdete logaritmus čísla.
Níže je uveden příklad:
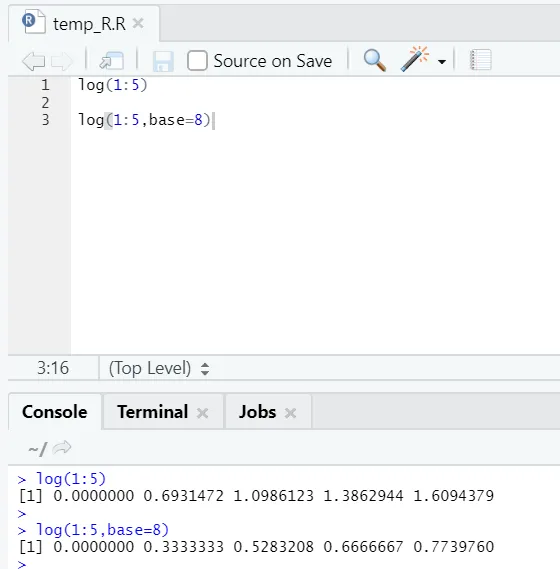
Zde člověk získá flexibilitu změnit základnu, podle požadavku.
f) Kumsum: Jedná se o matematickou funkci, která dává kumulativní součty. Zde je příklad níže:
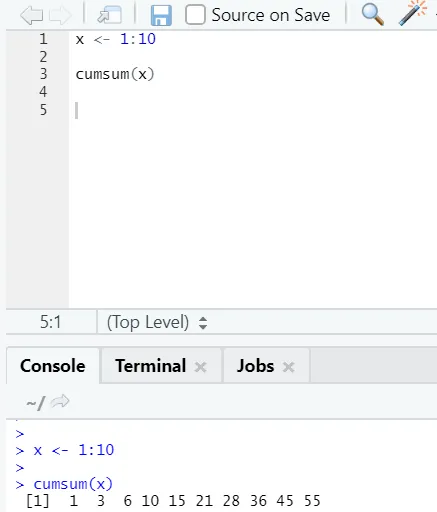
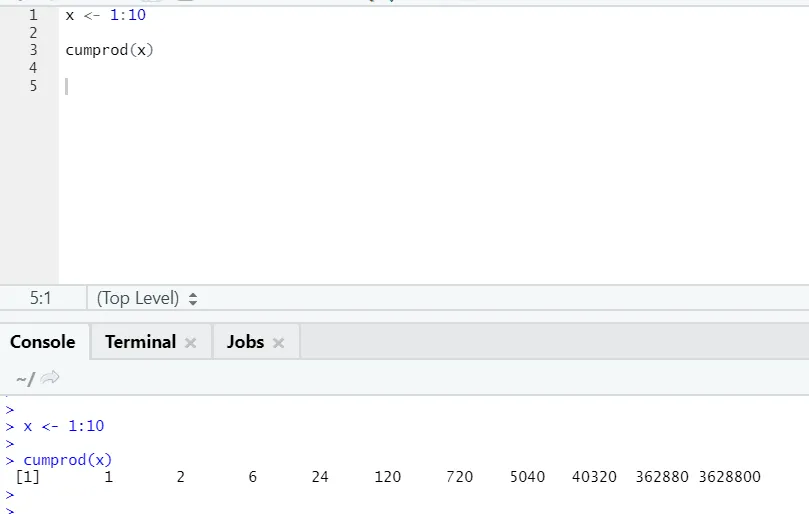
g) Cumprod: Stejně jako matematická funkce Cumsum, máme cumprod, kde dochází ke kumulativnímu násobení.
Viz níže uvedený příklad:
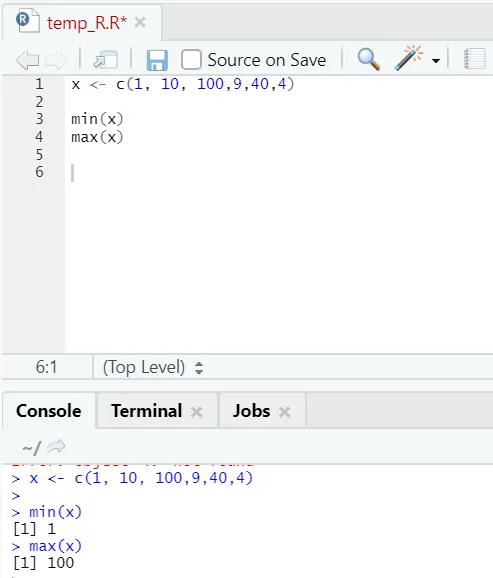
h) Max, Min: To vám pomůže najít maximální / minimální hodnotu v sadě čísel. Níže uvádíme příklady, které se k tomu vztahují:
i) Strop: Strop je matematická funkce, která vrací nejmenší celé číslo vyšší, než je uvedeno.
Podívejme se na příklad:
strop (2, 67)
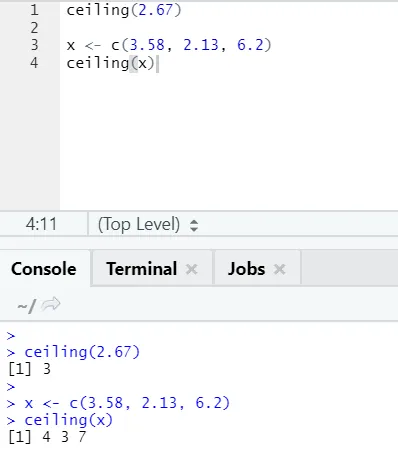
Jak si můžete všimnout, strop se aplikuje na číslo i na seznam a výstup přišel je nejmenší z dalšího vyššího celého čísla.
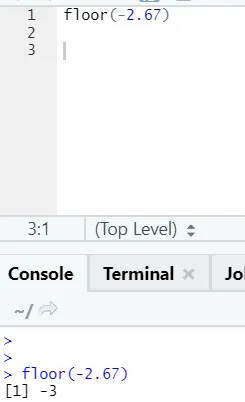
j) Patro: Patro je matematická funkce, která vrací nejmenší celé číslo zadaného čísla.
Níže uvedený příklad vám pomůže lépe porozumět:
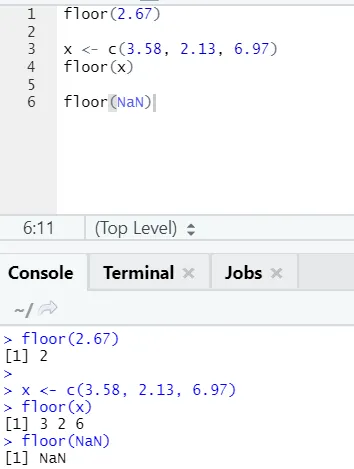
Stejně to funguje i pro záporné hodnoty. Prosím podívej se:
3) Statistické funkce -
Toto jsou funkce, které popisují související rozdělení pravděpodobnosti.
a) Medián: Vypočítá se medián ze sekvence čísel.
Syntax
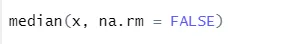
R kód a výstup:
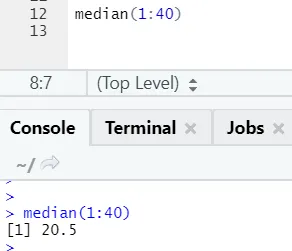
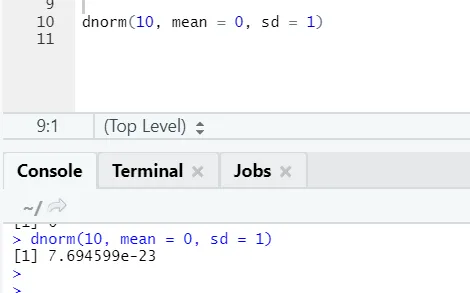
b) Dnorm: Jedná se o normální rozdělení. Funkce dnorm vrací hodnotu funkce hustoty pravděpodobnosti pro normální rozdělení dané parametry pro x, μ a σ.
R kód a výstup:
c) Cov: Covariance říká, zda dva vektory nejsou pozitivně, negativně nebo úplně nesouvisející.
R kód
x_new = c(1., 5.5, 7.8, 4.2, -2.7, -5.5, 8.9)
y_new = c(0.1, 2.0, 0.8, -4.2, 2.7, -9.4, -1.9)
cov(x_new, y_new)
R výstup:
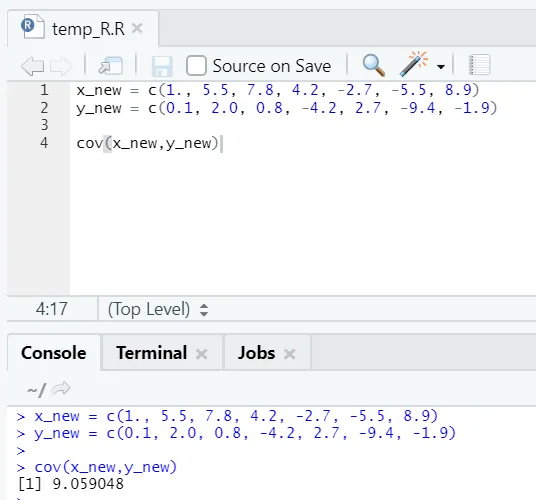
Jak vidíte, dva vektory mají pozitivní vztah, což znamená, že oba vektory se pohybují stejným směrem. Je-li kovariance záporná, znamená to, že xay jsou nepřímo související a tudíž se pohybují opačným směrem.
d) Cor: Toto je funkce k nalezení korelace mezi vektory. Ve skutečnosti dává asociační faktor mezi dvěma vektory, který je známý jako „korelační koeficient“. Korelace přidává stupeň koeficientu nad kovariancí. Pokud jsou dva vektory pozitivně korelovány, korelace vám také řekne, do jaké míry jsou pozitivně příbuzné.
Tyto tři typy metod, které lze použít k nalezení korelace mezi dvěma vektory:
- Pearsonova korelace
- Kendallova korelace
- Spearmanova korelace
V jednoduchém formátu R vypadá takto:
cor(x, y, method = c("pearson", "kendall", "spearman"))
Zde x a y jsou vektory.
Podívejme se na praktický příklad korelace přes vestavěný datový soubor.
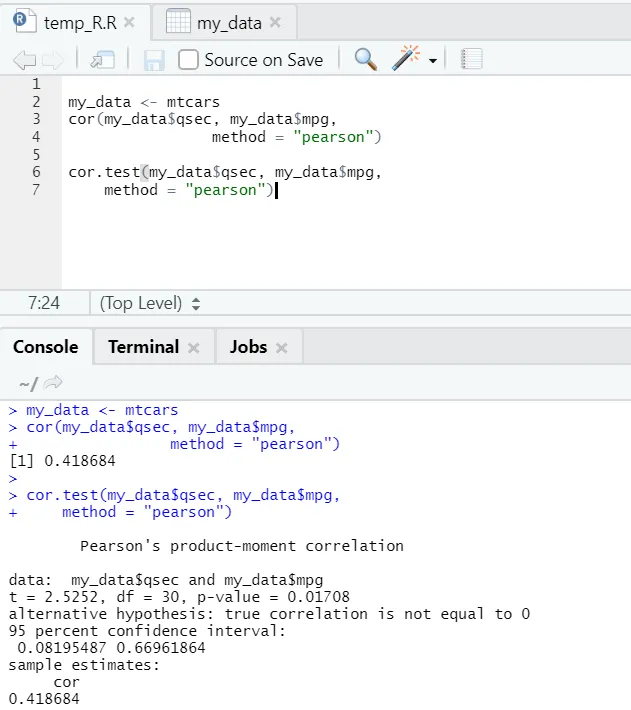
Tady tedy vidíte, že funkce „cor ()“ dala korelační koeficient 0, 41 mezi „qsec“ a „mpg“. Byla však představena ještě jedna funkce, tj. „Cor.test ()“, která nejen říká korelační koeficient, ale také p-hodnotu at. Interpretace je mnohem jednodušší s funkcí cor.test.
Podobné lze provést s dalšími dvěma způsoby korelace:
R kód pro Pearsonovu metodu:
my_data <- mtcars
cor(my_data$qsec, my_data$mpg, method = " pearson ")
cor.test(my_data$qsec, my_data$mpg, method = " pearson")
R kód pro Kendallovu metodu:
my_data <- mtcars
cor(my_data$qsec, my_data$mpg, method = " kendall")
cor.test(my_data$qsec, my_data$mpg, method = " kendall")
R kód pro Spearmanovu metodu:
my_data <- mtcars
cor(my_data$qsec, my_data$mpg, method = "spearman")
cor.test(my_data$qsec, my_data$mpg, method = "spearman")
Korelační koeficient se pohybuje mezi -1 a 1.
Pokud je korelační koeficient záporný, znamená to, že když x roste, y klesá.
Pokud je korelační koeficient nulový, znamená to, že mezi xay neexistuje žádná souvislost.
Pokud je korelační koeficient kladný, znamená to, že když x roste y, také má tendenci se zvyšovat.
e) T-test: T-test vám řekne, zda dva soubory dat pocházejí ze stejného (za předpokladu) normálního rozdělení nebo ne.
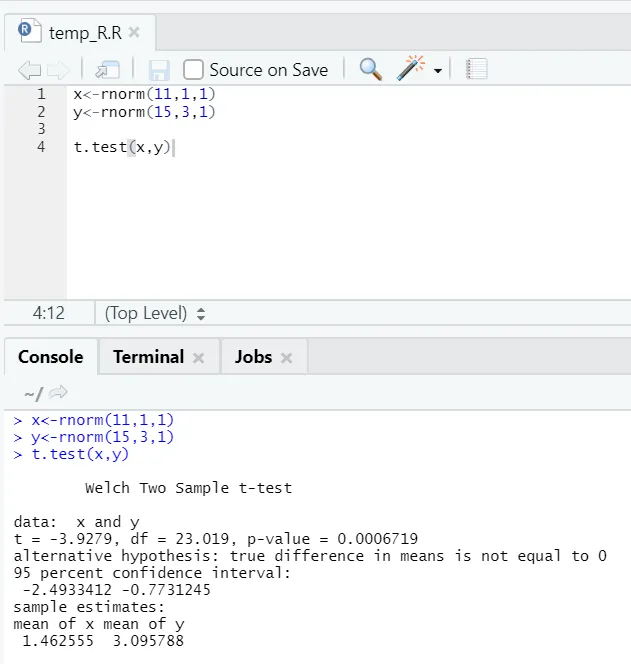
Zde byste měli odmítnout nulovou hypotézu, že dva prostředky jsou stejné, protože p-hodnota je menší než 0, 05.
Tato ukázaná instance je typu: nepárové datové sady s nestejnými odchylkami. Podobně lze vyzkoušet pomocí spárovaného datového souboru.
f) Jednoduchá lineární regrese: Toto ukazuje vztah mezi prediktorovou / nezávislou a odezvou / závislou proměnnou.
Jednoduchým praktickým příkladem by mohlo být předpovídání hmotnosti člověka, pokud je výška známa.
R syntaxe
lm(formula, data)
Zde vzorec znázorňuje vztah mezi výstupem tj. Y a vstupní proměnnou iex Data představují dataset, na který je třeba použít vzorec.
Podívejme se na jeden praktický příklad, kde podlahová plocha je vstupní proměnná a rent je výstupní proměnná.
x <- c (1510, 1000, 600, 500, 1280, 136, 1790, 1630)
y <- c (15000, 10000, 6000, 5000, 12800, 13600, 17900, 16300)
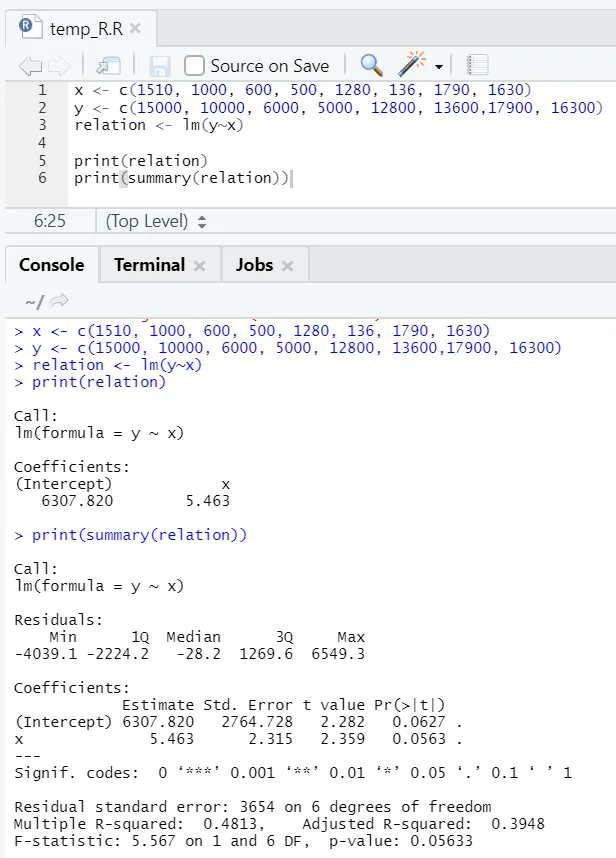
Zde není hodnota P menší než 5%. Nulovou hypotézu proto nelze odmítnout. Nemá velký význam prokázat vztah mezi podlahovou plochou a nájemným.
Zde je R-čtvercová hodnota 0, 4813. To znamená, že pouze 48% rozptylu ve výstupní proměnné lze vysvětlit vstupní proměnnou.
Řekněme, že nyní musíme předpovídat hodnotu podlahové plochy na základě výše uvedeného modelu.
R kód
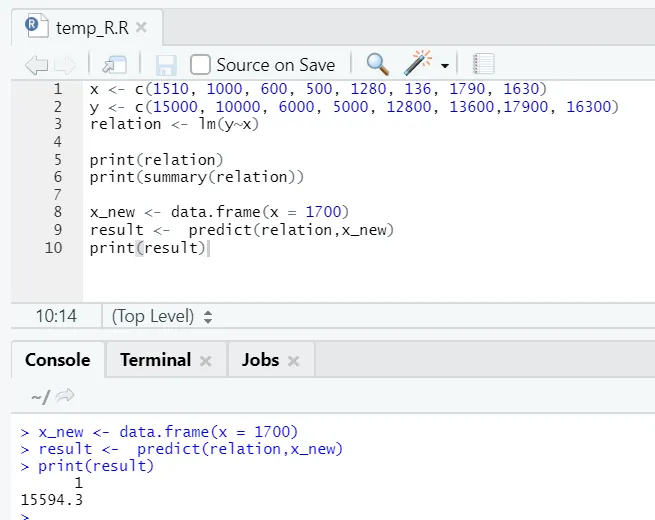
x_new <- data.frame(x = 1700)
result <- predict(relation, x_new)
print(result)
R výstup:
Po provedení výše uvedeného kódu R bude výstup vypadat takto:
Jeden může fit a vizualizovat regresi. Zde je kód R:
# Pojmenujte soubor grafu png.
png(file = "LinearRegressionSample.png.webp")
# Vykreslete graf.
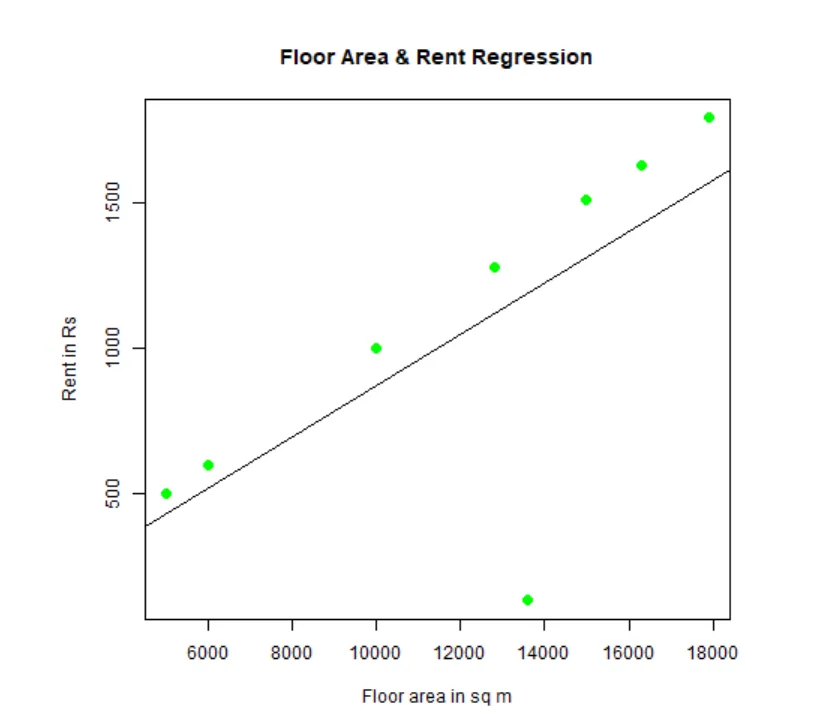
plot(y, x, col = "green", main = "Floor Area & Rent Regression",
abline(lm(x~y)), cex = 1.3, pch = 16, xlab = "Floor area in sq m", ylab = "Rent in Rs")
# Uložte soubor.
dev.off()
Tento graf „LinearRegressionSample.png.webp“ bude vygenerován v aktuálním pracovním adresáři.
g) Chi-Square test
Jedná se o statistickou funkci v R. Tento test má svůj význam, aby se prokázalo, zda existuje korelace mezi dvěma kategorickými proměnnými.
Tento test funguje také jako všechny ostatní statistické testy založené na p-hodnotě, lze akceptovat nebo odmítnout nulovou hypotézu.
R syntaxe
chisq.test(data), /code>
Podívejme se na jeden praktický příklad.
R kód
# Načíst knihovnu.
library(datasets)
data(iris)
# Vytvořte datový rámec z hlavní datové sady.
iris.data <- data.frame(iris$Sepal.Length, iris$Sepal.Width)
# Vytvořte tabulku s potřebnými proměnnými.
iris.data = table(iris$Sepal.Length, iris$Sepal.Width)
print(iris.data)
# Proveďte test na náměstí.
print(chisq.test(iris.data))
R výstup:
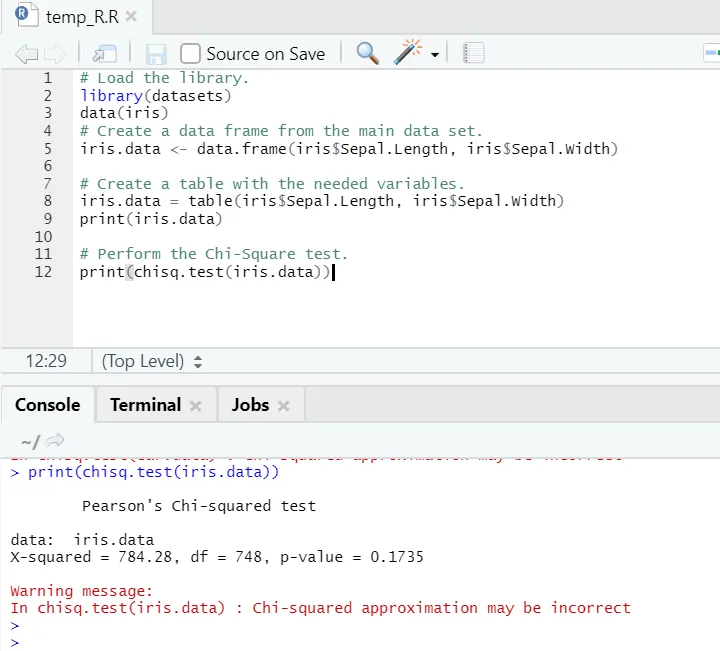
Jak je vidět, test chí-kvadrát byl proveden na datovém souboru duhovky s ohledem na jeho dvě proměnné „Sepal. Délka “a„ Sepal.Width “.
Hodnota p není menší než 0, 05, proto mezi těmito dvěma proměnnými neexistuje korelace. Nebo můžeme říci, že tyto dvě proměnné nejsou na sobě závislé.
Závěr
Funkce v R jsou jednoduché, snadno se přizpůsobí, snadno uchopí a přesto velmi silné. Viděli jsme řadu funkcí, které se používají jako součást základů v R. Jakmile se člověk s těmito funkcemi seznámí výše, můžeme prozkoumat jiné varianty funkcí. Funkce vám pomohou, aby váš kód běží jednoduše a stručně. Funkce mohou být vestavěny nebo definovány uživatelem, vše záleží na potřebě při řešení problému. Funkce dávají programu dobrý tvar.
Doporučené články
Toto je průvodce funkcemi v R. Zde diskutujeme, jak psát funkce v R a různé typy funkcí v R se syntaxí a příklady. Další informace naleznete také v následujícím článku -
- R Řetězcové funkce
- Funkce SQL String
- Funkce řetězce T-SQL
- Funkce PostgreSQL String