
Úvod do rekurzivní funkce v C ++
Pro začátek rekurzivní funkce v C ++ jsme již znali základní myšlenku funkcí C ++, která zahrnuje definici funkce pro volání dalších funkcí. A tento článek se zabývá konceptem rekurzivní definice, konceptem nástroje pro hraní v matematice a programovací logice. Známý příklad zahrnuje faktoriál čísla, součet přirozených čísel „n“ atd. Funkce, která sama volá, je známá jako rekurzivní funkce. Jsou to jen funkce, která se opakovaně vyvolává. Rekurze má nástroj pro řešení problémů, kde rozděluje větší problémy do jednoduchých úkolů a pracuje individuálně, aby sledoval jednotlivé posloupnosti.
Koncepty datových struktur, jako je vyhledávání, třídění, procházení stromu, využívají rekurzivní funkce pro svá řešení. Tato programovací technika usnadňuje kód. Jak iterace, tak rekurze dělají stejný proces jako opakování kódu, ale rozdíl v rekurzi spočívá v tom, že vykonávají určitou část se samotnou základní funkcí. V tomto článku probereme důležitost rekurze a jejich pracovní postup s podrobným příkladem.
Syntax rekurzivní funkce v C ++
Obecná syntax rekurzivní funkce v c ++ je dána jako:
return type function name((arguments))
(
Body of the statements;
function name ((actual arguments)) // recursive function
)
Jak funguje rekurzivní funkce v C ++?
Rekurze provádí opakování volání funkcí a zastaví provádění, když se základní případ stane skutečností. V rekurzivní funkci by měla být definována podmínka základního případu, aby se zabránilo chybové zprávě o přetečení zásobníku. Pokud není definován žádný základní případ, vede to k nekonečné rekurzi. Když je funkce volána, posouvá je do zásobníku pokaždé pro rezervování zdrojů pro každé opakované volání. Dává to nejlepší při stromovém průniku. Existují dva různé typy rekurze: přímá a nepřímá rekurze.
Přímé rekurzivní: Ilustrace
int fibn(n)
(
fib(n);
)
void main ()
(
fib(n);
)
Výše uvedený formát je přímé rekurzivní volání, kde okamžitě volá / volá sám. Zvažte druhý typ nazvaný nepřímá rekurze, který zahrnuje další volání funkce. Je vidět na následujícím obrázku:
Nepřímý rekurzivní: Ilustrace
void f(int n) (
f1();
return;
)
void f2( int n) (
f();
return;
)
void f1() (
f2();
return;
)
Příklady rekurzivní funkce v C ++
V níže uvedeném programu můžete vidět provedení programu, který jsem poskytl s výchozí základní podmínkou. Někdy použití stavu if-else při rekurzi pomáhá zabránit nekonečné rekurzi. Proces kódu se provádí s částečným řešením v meziproduktu a ty se spojí do konečného řešení při rekurzi ocasu.
Příklad č. 1
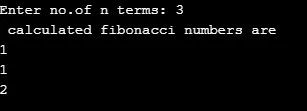
Zde je jednoduchý příklad řady Fibonacciho čísla. Níže uvedený program zahrnuje volání rekurzivní funkce definované jako fib (int n), které přebírá vstup od uživatele a ukládá jej do 'n'. Další krok zahrnuje převzetí smyčky pro generování termínu, který je předán funkční fib () a vrací Fibonacciho řadu. Základní případ je nastaven příkazem if kontrolou čísla = 1 nebo 2, aby se vytiskly první dvě hodnoty. Nakonec tato rekurzivní funkce pokračuje se smyčkou pro tisk série 1, 1, 2.
Kód:
#include
using namespace std;
int fib_r (int s)
(
if(s==1||s==2)
return 1;
else
return (fib_r(s-1) +fib_r(s-2)); // fib(n-1) + fib(n-2) for adding successive terms
)
int main ()
(
int k, n;
cout<<"Enter no.of n terms: ";
cin>>n;
cout<<" calculated fibonacci numbers are"< for (k=1; k<=n; k++)
cout< return 0;
)#include
using namespace std;
int fib_r (int s)
(
if(s==1||s==2)
return 1;
else
return (fib_r(s-1) +fib_r(s-2)); // fib(n-1) + fib(n-2) for adding successive terms
)
int main ()
(
int k, n;
cout<<"Enter no.of n terms: ";
cin>>n;
cout<<" calculated fibonacci numbers are"< for (k=1; k<=n; k++)
cout< return 0;
)#include
using namespace std;
int fib_r (int s)
(
if(s==1||s==2)
return 1;
else
return (fib_r(s-1) +fib_r(s-2)); // fib(n-1) + fib(n-2) for adding successive terms
)
int main ()
(
int k, n;
cout<<"Enter no.of n terms: ";
cin>>n;
cout<<" calculated fibonacci numbers are"< for (k=1; k<=n; k++)
cout< return 0;
)
Výstup:
Příklad č. 2
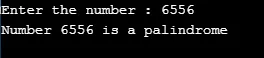
Kontrola čísla palindromu pomocí rekurzivní funkce.
Kód:
#include
using namespace std;
int palim(int a, int t)
(
if (a == 0)
return t;
t = (t * 10) + (a % 10);
return palim(a / 10, t);
)
int main()
(
int n;
cout<>n;
int result = palim(n, 0);
if (result == n)
cout << "Number "< else
cout << "Number "< return 0;
)#include
using namespace std;
int palim(int a, int t)
(
if (a == 0)
return t;
t = (t * 10) + (a % 10);
return palim(a / 10, t);
)
int main()
(
int n;
cout<>n;
int result = palim(n, 0);
if (result == n)
cout << "Number "< else
cout << "Number "< return 0;
)#include
using namespace std;
int palim(int a, int t)
(
if (a == 0)
return t;
t = (t * 10) + (a % 10);
return palim(a / 10, t);
)
int main()
(
int n;
cout<>n;
int result = palim(n, 0);
if (result == n)
cout << "Number "< else
cout << "Number "< return 0;
)
Výstup:
Příklad č. 3
Programujte pomocí generátoru náhodných čísel.
Kód:
#include
#include
#include
#include
using namespace std;
int rand1(int n);
int main () (
int n, j;
int r;
srand(time (NULL));
cout << "Enter number of dice: ";
cin >> n;
for (j = 1; j <= n; j++) (
r = rand1(5) + 1;
cout << r << " ";
)
system("PAUSE");
return 0;
)
int rand1(int n) (
return rand () % n;
)
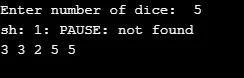
Výše uvedený program ilustruje generátor náhodných čísel, když se kostky náhodně hodí. Provádí se vyvoláním funkce rand1 (int n) a vygeneruje 0 až n-1 čísla. a nastavení počáteční hodnoty s nulovou hodnotou (bez adresy). Například, pokud zadáme jako 4, vyvolá to kostky jako 5, 4, 1, 2.
Výstup:
Existují také některé pojmy, jako je lineární vyhledávání, společný dělitel a nejdůležitější faktoriál daného čísla, které využívá rekurzivní implementaci.
Pros rekurze
- Kód, který poskytují, je čistý a kompaktní zjednodušením rozsáhlejšího komplexního programu. V programovém kódu používá méně proměnných.
- Zde se vyhneme složitému kódu a vnořenému pro smyčky.
- Některá část kódu vyžaduje zpětné sledování, které je řešeno rekurzivně.
Nevýhody rekurze
- Zabere více přidělení paměti díky operaci zásobníku všech volání funkcí.
- Během provádění iteračního procesu někdy pracuje pomaleji. Proto je účinnost menší.
- Pro začátečníky je obtížné porozumět práci, protože kód někdy přechází do hloubky. pokud vede k nedostatku místa a nakonec způsobí zhroucení programu.
Závěr
S tím jsme diskutovali o tom, jak funkce c ++ fungují a definují rekurzivně. A my jsme prošli korespondcí a jejich klady a zápory rekurzivní funkce ve světě programování. Poté jsme pokračovali ukázáním, jak může být implementována v C ++ pomocí rekurzivní definice funkce. Dále jsme dospěli k závěru, že rekurze pomáhá v C ++ řešit problémy v pojmech datové struktury, jako jsou traversals, třídění a vyhledávání, a lze je efektivně použít všude tam, kde je to potřeba.
Doporučené články
Toto je průvodce rekurzivní funkcí v C ++. Zde diskutujeme, jak rekurzivní funkce funguje v C ++, syntaxi spolu s různými příklady a implementací kódu. Další informace naleznete také v následujících článcích -
- Co jsou funkce C ++ Array?
- Přehled funkcí řetězce C ++
- Nejlepší kompilátor C ++ (příklady)
- Úvod do příkazů C ++
- Fibonacciho řada v Javě
- Generátor náhodných čísel v Matlabu
- Generátor náhodných čísel v C #
- Palindrom v C ++
- Generátor náhodných čísel v JavaScriptu
- Prvních 11 funkcí a výhod C ++
- Naučte se typy funkcí polí v PHP