
Úvod do rekurzivní funkce v Javě
Rekurzivní funkce je ta, která se sama volá nebo mnohokrát. Rekurzivní funkce se používá v situacích, kdy je třeba znovu a znovu provádět stejnou sadu operací, dokud není dosaženo výsledku. Provádí několik iterací a prohlášení o problému se s každou iterací stále zjednodušuje.
Při psaní rekurzivní funkce musí být vždy zadán základní limit, jinak dojde k chybě přetečení zásobníku. Zásobník je oblast paměti vyhrazená pro udržování vyvolávání metod. Tato chyba je způsobena tím, že funkce začíná provádět nepřetržitě, protože nebude schopna najít limitující podmínku, a tím konečně vyčerpá přidělenou paměť. Abychom zabránili přetečení zásobníku, definujeme určité základní podmínky pomocí příkazů „if… else“ (nebo jiných podmíněných příkazů), díky nimž se rekurzní funkce zastaví, jakmile je požadovaný výpočet dokončen.
Typy rekurze v Javě
V Javě existují 2 typy rekurze. Oni jsou:
1. Přímá rekurze
Syntax:
Zde funkce1 volá sama sebe, a proto je rekurzivní funkce.
public static void main(String() args)(
//few lines of code
function();
//few lines of code
)
function() (
//few lines of code
function();
//few lines of code
)
Příklad
Příkladem přímé rekurze je Factorial of number. Základním principem rekurze je vyřešit složitý problém rozdělením na menší. Například v případě faktoriálu čísla vypočítáme faktoriál „i“, pokud známe jeho faktoriál „i-1“.
Kód:
public class Factorial (
static int fact(int i)(
if (i == 1)
return 1;
else
return(i * fact(i-1));
)
public static void main(String() args) (
System.out.println("The factorial of given number 6 is: "+fact(6));
)
)
Výstup:

2. Nepřímá / vzájemná rekurze
Funkce1, která volá jinou funkci2, která na oplátku volá funkci1 přímo nebo nepřímo, se nazývá nepřímá rekurzivní funkce.
Syntax:
Zvažte 2 funkce nazvané function1 () a function2 (). Zde funkce1 volá funkci2 a funkce2 volá funkci1.
function1()(
//few lines of code
function2();
//few lines of code
)
function2()(
//few lines of code
function1();
//few lines of code
)
Příklad
Abychom ukázali nepřímou rekurzi, vezmeme následující program, abychom zjistili, zda je dané číslo od daného vstupu sudé nebo liché.
Kód:
import java.util.Scanner;
public class IndirectRecursion (
public static boolean oddNum(int i) (
if (i<0) throw new IllegalArgumentException("Number is negative");
if(i == 0)(
return false;
) else (
return evenNum(i-1);
)
)
public static boolean evenNum(int i) (
if (i<0) throw new IllegalArgumentException("Number is negative");
if(i == 0)(
return true;
) else (
return oddNum(i-1);
)
)
public static void main(String() args) (
Scanner inputNum = new Scanner(System.in);
System.out.print("Give a number: ");
int n = inputNum.nextInt();
if (evenNum(n)) System.out.println(n + " is even");
else System.out.println(n + " is odd");
inputNum.close();
)
)
Výstup:
Příklady rekurze v Javě
Zde je několik dalších příkladů řešení problémů pomocí metody rekurze.
Příklad č. 1 - Fibonacciho sekvence
Řada čísel „n“ je označována jako sekvence Fibonacci, pokud číslo 3 = číslo1 + číslo2, tj. Každé číslo je součtem předchozích dvou čísel. Proto sekvence vždy začíná prvními dvěma číslicemi jako 0 a 1. Třetí číslice je součet 0 a 1, což má za následek 1, čtvrté číslo je sčítání 1 a 1, což má za následek 2 a posloupnost pokračuje.
Chcete-li vygenerovat Fibonacciho sekvenci, podívejte se na následující kód v Javě:
public class FibonacciSeries(
static int num1=0, num2=1, num3=0;
static void fibonacci(int n)(
if(n>0)(
num3 = num1 + num2;
num1 = num2;
num2 = num3;
System.out.print(" "+num3);
fibonacci(n-1);
)
)
public static void main(String args())(
int n=10;
System.out.print(num1+" "+num2);//printing constant first two digits 0 and 1
fibonacci(n-2);//Since first two numbers are already done
)
)
Výstup:

Zde jsou první dvě čísla inicializována na 0 a 1 a vytištěna. Proměnné „num1“, „num2“ a „num3“ se používají ke generování požadované sekvence. Proměnná „num3“ se získá přičtením „num1“ a „num2“ a čísla se posunou o jednu pozici doleva zamícháním, jak ukazuje kód. Funkce „Fibonacci“ se zde rekurzivně nazývá a při každé iteraci se hodnota „n“ sníží o 1. Proto rekurze skončí, jakmile „n“ dosáhne hodnoty 0.
Příklad č. 2 - Hanojská věž
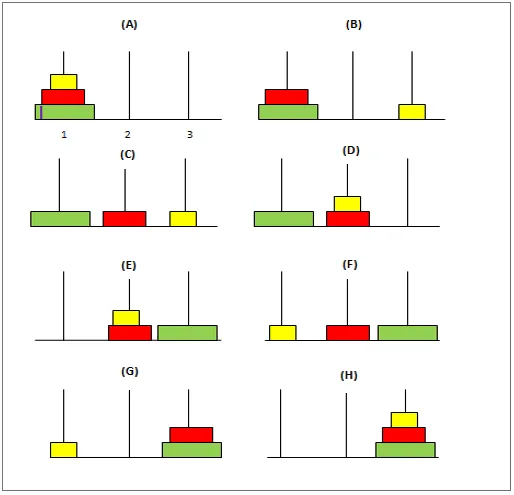
Jedná se o klasický matematický problém, který má 3 póly a „n“ počet disků různých velikostí. Hádanka vypadá takto:
Na začátku bude první tyč mít disky uspořádané tak, že největší disk z nich je dole a nejmenší v horní části sloupu. Cílem je přesunout tyto disky z prvního pólu do třetího pólu a udržet je ve stejné poloze jako v prvním. Při přemisťování těchto disků je třeba mít na paměti několik podmínek:
1. Najednou je nutné přesunout pouze jeden disk.
2. V tomto procesu není dovoleno umisťovat větší disk na menší.
3. Druhý (prostřední) pól může být použit pro zprostředkování při přenosu disků z prvního na druhý pól.
Následuje kód Java, který lze použít k vyřešení hádanky:
Kód:
public class TowerOfHanoi (
public static void main(String() args) (
int count = 3;
tower(count, 'A', 'B', 'C');
)
public static void tower(int first, char disk1, char temp, char disk2) (
if (first == 1) (
System.out.println("Disk 1 from " + disk1 + " to " + disk2);
) else (
tower(first - 1, disk1, disk2, temp);
System.out.println("Disk " + first + " from " + disk1 + " to " + disk2);
tower(first - 1, temp, disk1, disk2);
)
)
)
Výstup:
Proměnná „počet“ zde představuje počet disků, které mají být použity. Funkce „věž“ je rekurzivní funkce používaná k přemísťování disků z tyče 1 na tyč 3. Jednoduché řešení tohoto problému může být zajištěno tím, že nejprve vezmeme v úvahu 2 disky.
- Nejprve začneme přesunutím disku 1 z tyče 1 do tyče 2.
- Dále přesuneme disk2 na tyč 3.
- Nakonec dokončíme přesunutím disku 1 na tyč 3, čímž dokončíme požadované řešení.
Stejný princip se použije pro „n“ počet disků přesunutím (n-1) disku z tyče 1 na 2 a následováním podobných kroků jako výše.
Výhody rekurze v Javě
- Kód lze snadno zapisovat a udržovat.
- Nejlepší metoda k nalezení výsledků tam, kde je vyžadováno velké množství iterací.
Nevýhody rekurze v Javě
- Rekurzivní funkce využívají více paměti. Je to proto, že při každém vyvolání rekurzivní funkce; přidělení paměti se provádí nově pro proměnné v zásobníku. Jakmile je vrácena hodnota proměnné, je uvolněno příslušné přidělení paměti.
- Tento proces přidělení paměti zabere více času, a proto je provádění obvykle pomalé.
Závěr
Rekurzivní funkce jsou relativně jednodušší pro kódování, ale také nejsou tak účinné ve srovnání s jinými stávajícími metodami. Používají se proto hlavně v případech, kdy je čas potřebný k vývoji kratší a také v případech, kdy lze v problému pozorovat významný vzorec.
Doporučené články
Toto je průvodce rekurzí v Javě. Zde diskutujeme typy rekurze v Javě a její různé příklady s výhodami a nevýhodami. Další informace naleznete také v následujících článcích
- JScrollPane v Javě
- Matematické funkce v Javě
- Matematické funkce v Javě
- Konstruktor v Javě
- Rekurzivní funkce v Pythonu
- Věcný program v JavaScriptu