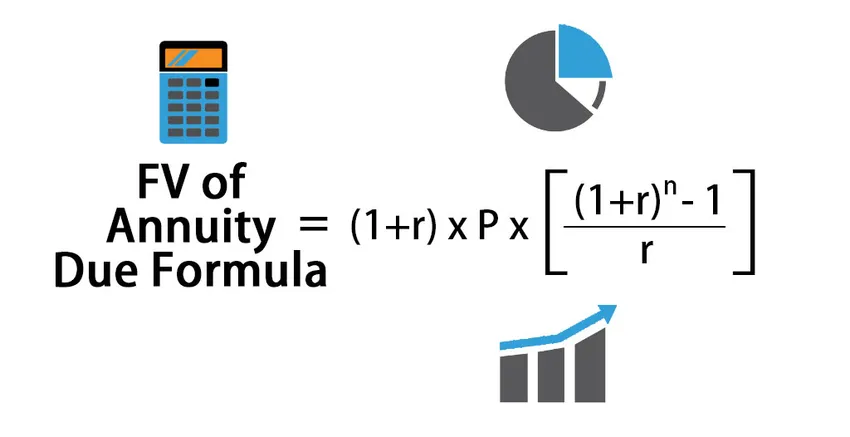
Budoucí hodnota anuity Due Formula (obsah)
- Budoucí hodnota anuity Due Formula
- Příklady budoucí hodnoty vzorce důchodu (s šablonou Excel)
- Budoucí hodnota anuity Due Formula Calculator
Budoucí hodnota anuity Due Formula
Vzorec pro výpočet budoucí hodnoty splatné anuity:
FV of Annuity Due = (1+r) * P * (((1+r) n – 1) / r )
Kde,
- P = periodická platba
- R = sazba za období
- N = počet období
Příklady budoucí hodnoty vzorce důchodu (s šablonou Excel)
Vezměme si příklad, abychom lépe pochopili výpočet budoucí hodnoty splatnosti anuity.
Zde si můžete stáhnout tuto šablonu Excel pro budoucí hodnotu anuity díky vzorci - Budoucí hodnotu šablony pro anuitu kvůli vzorciPříklad č. 1
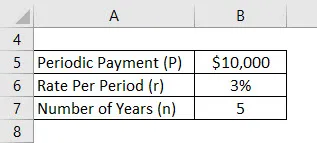
Předpokládejme, že Anand vložil 10 000 $ ročně a efektivní sazba, kterou jeho účet nabízí, je 3%. Nyní chce Anand vypočítat svůj budoucí zůstatek po 5 letech s předpokládaným prvním vkladem od dnešního dne.
Řešení:
Budoucí hodnota splatnosti anuity se vypočítá pomocí vzorce uvedeného níže
FV splatnosti anuity = (1 + r) * P * (((1 + r) n - 1) / r)
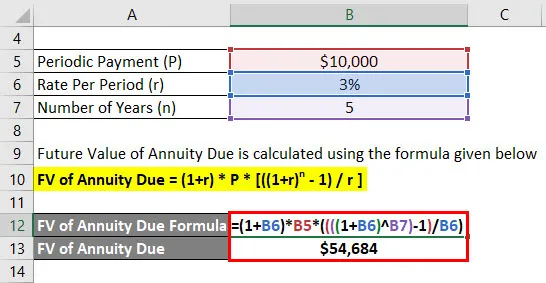
- FV splatnosti anuity = (1+ 3%) * 10 000 * * (((((1 + 3%) 5) - 1) / 3%)
- FV splatné anuity = 54 684 $
Anand získá 54 684 $ budoucí zůstatek po 5 letech.
Příklad č. 2
Předpokládejme, že Jagriti vložilo 8 000 $ ročně a efektivní sazba, kterou jeho účet nabízí, je 5%. Nyní chce Jagriti vypočítat svůj budoucí zůstatek po 5 letech, přičemž předpokládá první vklad od dnešního dne.

Řešení:
Budoucí hodnota splatnosti anuity se vypočítá pomocí vzorce uvedeného níže
FV splatnosti anuity = (1 + r) * P * (((1 + r) n - 1) / r)
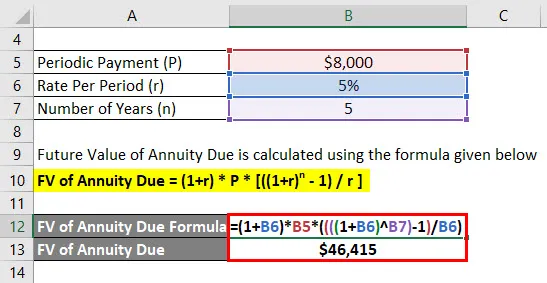
- FV splatnosti anuity = (1+ 5%) * 8 000 $ * (((((1 + 5%) 5) - 1) / 5%)
- FV splatné anuity = 46 415 $
Jagriti získá budoucí zůstatek ve výši 46 415 $ po 5 letech.
Příklad č. 3
Předpokládejme, že Anandriti vložil 20 000 $ ročně a efektivní sazba, kterou jeho účet nabízí, je 2%. Nyní chce Anandriti vypočítat svůj budoucí zůstatek po 5 letech, přičemž předpokládá první vklad od dnešního dne.
Řešení:
Budoucí hodnota splatnosti anuity se vypočítá pomocí vzorce uvedeného níže
FV splatnosti anuity = (1 + r) * P * (((1 + r) n - 1) / r)
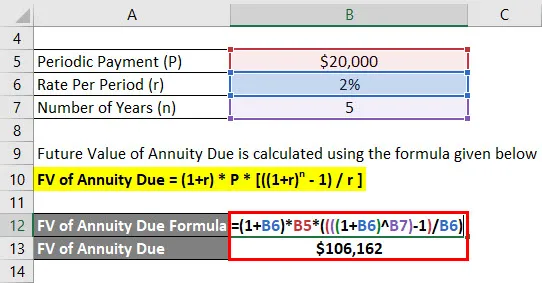
- FV splatnosti anuity = (1+ 2%) * 20 000 $ * (((((1 + 2%) 5) - 1) / 2%)
- FV splatné anuity = 1 066 162 $
Anandriti získá budoucí zůstatek ve výši 1 06 162 $ po 5 letech.
Vysvětlení
Pro výpočet konečné hodnoty řady peněžních toků nebo platby, kde je první splátka obdržena okamžitě, použijeme budoucí hodnotu splatné anuity. První okamžitá splátka nebo platba rozlišují anuitu způsobenou běžnou anuitou. Okamžitá nebo okamžitá anuita se označuje jako splatná anuita.
Vypočítá hodnotu peněžních toků v budoucím období. Použití FV splatné anuity se v reálných situacích liší od současné hodnoty splatné anuity. Předpokládejme například, že společnost nebo jednotlivec kupuje anuitu a dnes zaplatil první splátku. Pomocí tohoto příkladu můžeme dále vysvětlit, předpokládat, že společnost nebo jednotlivec chce od kohokoli koupit anuitu a dnes provedl první platbu. Pro výpočet ceny, kterou je třeba v této situaci zaplatit, můžeme použít současnou hodnotu vzorce rentability. Pokud však chceme vypočítat zbývající zůstatek po uložení úroku po dobu 5 let na účtu a rozhodli jsme se vyplatit první splátku dnes, v tomto případě se použije budoucí hodnota anuity. Splatnost anuity lze vysvětlit jako druh anuity, kde peněžní toky nastávají na začátku každého období. Vzhledem k pokročilé povaze peněžních toků podléhá každý peněžní tok složenému efektu pro každé další období, pokud je porovnán s běžnou anuitou. Budoucí hodnota běžné anuity je nižší než budoucí hodnota anuity, protože budoucí hodnota anuity získává periodický úrok faktoru jedna plus.
Relevance a použití budoucí hodnoty splatné důchodu
Pojďme pochopit význam budoucí hodnoty a anuity splatné samostatně. Budoucí hodnotu lze vysvětlit jako celkovou hodnotu pro částku v hotovosti, která má být v budoucnu zaplacena k určitému datu. A splatnou anuitu lze vysvětlit jako sérii plateb, která se provádí na začátku každého období v pravidelném pořadí. Budoucí hodnotu splatné anuity lze proto vysvětlit jako celkovou hodnotu k určitému budoucímu datu pro řadu systematických / pravidelných plateb, pokud se platby provádějí na začátku každého období. Tento typ transakce a takový tok plateb lze vidět na účtu příjemce penzijního plánu. Celková hodnota je částka, do které se řada plateb provedených v budoucím datu zvýší, jakmile se předpokládá určitá výše úroků, a výnosy se v průběhu určitého období postupně zvyšují. Výpočet budoucí hodnoty běžné anuity je totožný s tím, ale jediným rozdílem je, že přidáme dodatečné období platby, které se provádí na začátku.
Budoucí hodnota anuity Due Formula Calculator
Můžete použít následující budoucí kalkulaci anuity Due Calculator
| P | |
| r | |
| n | |
| Budoucí hodnota anuity Due Formula | |
| Budoucí hodnota anuity Due Formula = | (1 + r) * P * (((1 + r) n - 1) / r) |
| = | (1 +0) * 0 * (((1 +0) 0 -1) / 0) = 0 |
Doporučené články
Toto byl průvodce pro budoucí hodnotu Formule anuity. Zde diskutujeme, jak vypočítat budoucí hodnotu anuity Due spolu s praktickými příklady. Rovněž poskytujeme kalkulačku budoucí hodnoty anuity Due s šablonou Excel ke stažení. Další informace naleznete také v následujících článcích -
- Průvodce časovou hodnotou peněz
- Příklady vzorce faktoru současné hodnoty
- Kalkulačka pro výpočet poměru informací
- Vzorec pro stupeň provozní páky