
Koeficient variační rovnice (obsah)
- Vzorec
- Příklady
Co je variační koeficient?
Ve statistice je variační koeficient také nazýván CV jako nástroj, který nám pomáhá určit, jak jsou datové body v sadě dat distribuovány kolem střední hodnoty. V zásadě jsou nejprve vyneseny všechny datové body a poté je variační koeficient použit k měření rozptylu těchto bodů od sebe a střední hodnoty. Pomáhá nám to pochopit data a také vidět vzorec, který tvoří. Vypočítá se jako poměr směrodatné odchylky sady dat ke střední hodnotě. Vyšší variační koeficient znamená, že existuje větší rozptyl dat kolem střední hodnoty. Podobně čím nižší je hodnota variačního koeficientu, tím menší je rozptyl a výsledky budou přesnější. I když průměr dvou datových řad je značně odlišný, variační koeficient je velmi užitečný pro srovnání stupně variace z jedné datové řady do druhé.
Vzorec pro variační koeficient je dán:
Coefficient of Variation = Standard Deviation / Mean
Kroky pro výpočet variačního koeficientu:
Krok 1: Vypočítejte průměr ze sady dat. Průměr je průměr všech hodnot a lze jej spočítat součtem všech hodnot a poté dělením počtem datových bodů.
Krok 2: Poté vypočítejte směrodatnou odchylku sady dat. To je trochu časově náročný proces. Směrodatná odchylka může být vypočtena jako: √ (Σ (X i - X m ) 2 / (n - 1)) . X i je i-tý datový bod a X m je průměr sady dat. Alternativně můžeme také najít standardní odchylku v Excelu pomocí funkce STDEV.S ().
Krok 3: Rozdělte směrodatnou odchylku střední hodnotou, abyste získali variační koeficient.
Příklady vzorce variačního vzorce (se šablonou Excel)
Vezměme si příklad, abychom lépe pochopili výpočet variačního koeficientu.
Tuto šablonu koeficientu variačního vzorce Excel si můžete stáhnout zde - šablonu koeficientu variačního vzorce ExcelKoeficient variační rovnice - Příklad č. 1
Řekněme, že máme dvě datové sady A a B a každá obsahuje 20 náhodných datových bodů. Vypočítejte variační koeficient pro datový soubor X & Y.
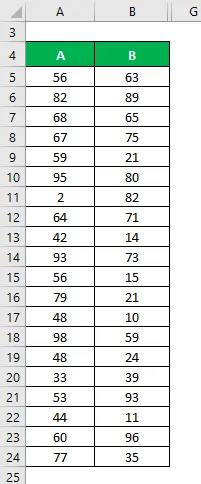
Řešení:
Průměr se počítá jako:
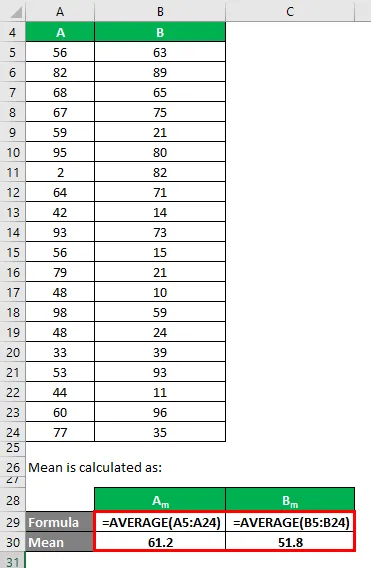
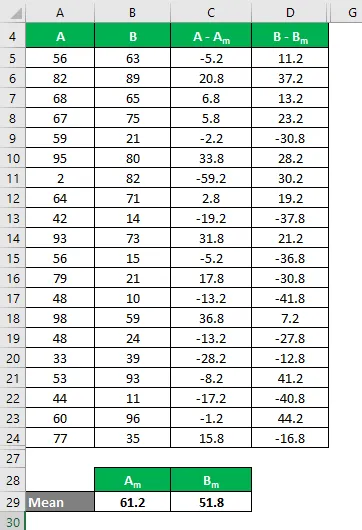
- Průměrná sada dat A = 61.2
- Průměrná sada dat B = 51, 8
Nyní musíme vypočítat rozdíl mezi datovými body a střední hodnotou.
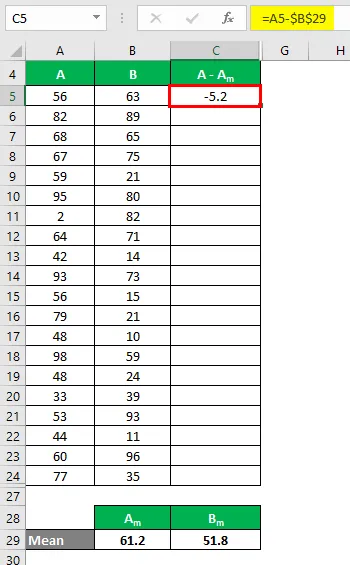
Podobně vypočítejte pro všechny hodnoty datové sady A.
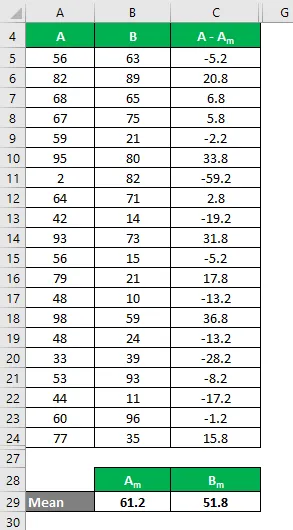
Podobně vypočítejte pro všechny hodnoty sady dat B.
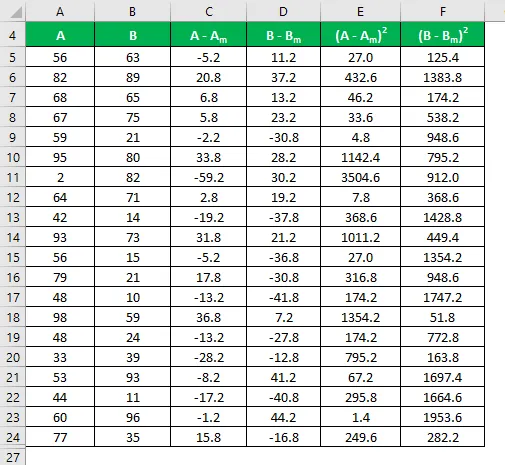
Vypočítejte druhou mocninu rozdílu pro oba soubory dat A a B.
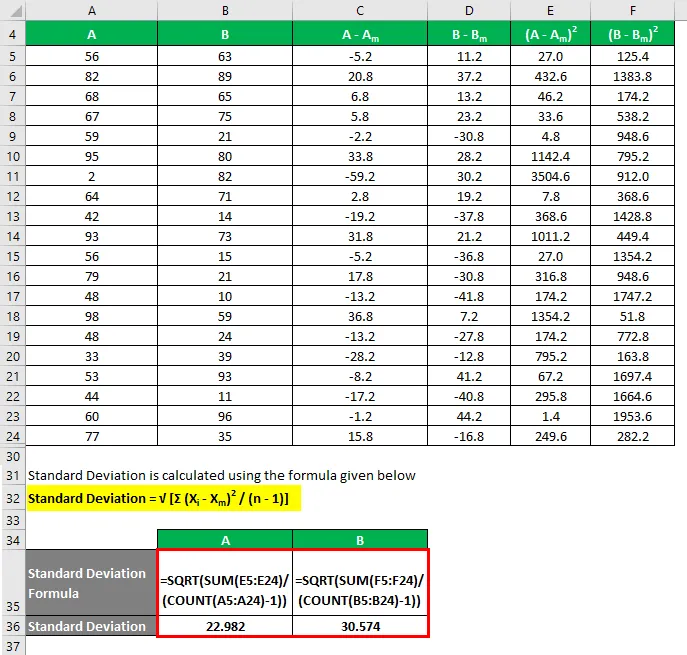
Standardní odchylka se vypočítá pomocí vzorce uvedeného níže
Směrodatná odchylka = √ (Σ (X i - X m ) 2 / (n - 1))
Variační koeficient se vypočítá pomocí vzorce uvedeného níže
Variační koeficient = standardní odchylka / průměr
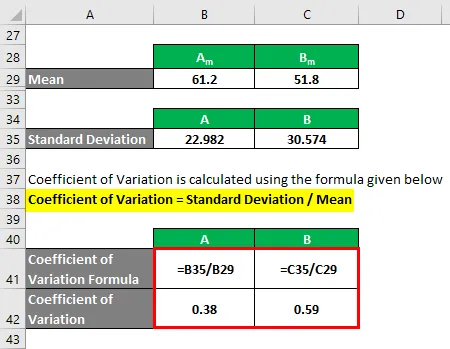
- Variační koeficient A = 22, 982 / 61, 2 = 0, 38
- Variační koeficient B = 30, 574 / 51, 8 = 0, 59
Takže pokud zde vidíte, B má vyšší variační koeficient než A, což znamená, že datové body B jsou rozptýlenější než A.
Koeficient variační rovnice - Příklad č. 2
Řekněme, že jste velmi averzní investor a chcete investovat peníze na akciovém trhu. Protože vaše riziková chuť k jídlu je nízká, chcete investovat do bezpečných akcií, které mají nižší směrodatnou odchylku a variační koeficient. Vybrali jste užší seznam 3 akcií na základě jejich základních a technických informací a chcete si vybrat 2 akcie. Shromažďovali jste také informace o jejich historických návratech za posledních 15 let.
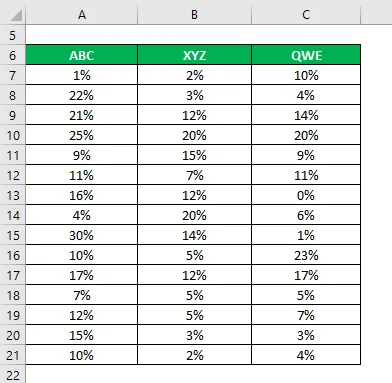
Řešení:
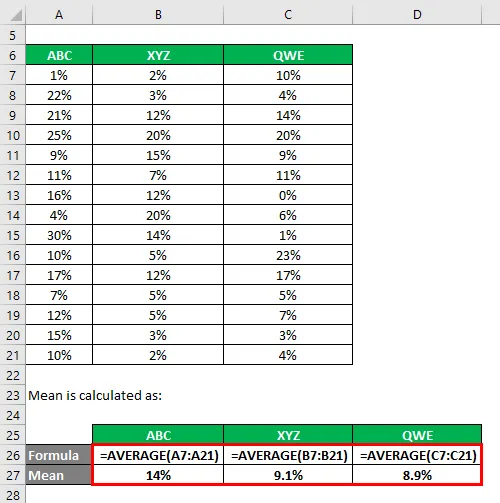
Průměr se počítá jako:
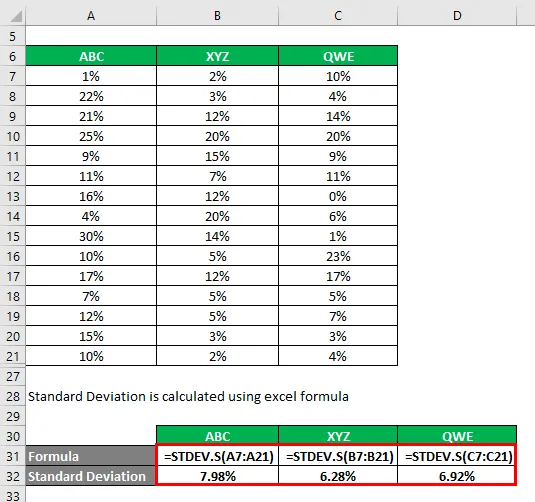
Standardní odchylka se počítá pomocí Excelu
Variační koeficient se vypočítá pomocí vzorce uvedeného níže
Variační koeficient = standardní odchylka / průměr
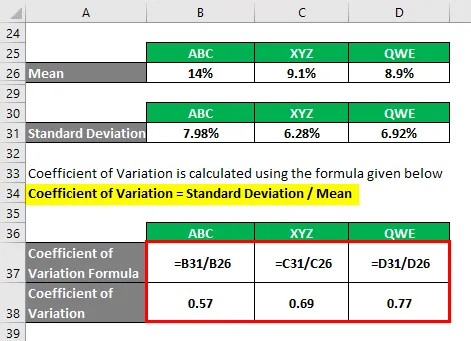
- Variační koeficient ABC = 7, 98% / 14% = 0, 57
- Variační koeficient XYZ = 6, 28% / 9, 1% = 0, 69
- Variační koeficient QWE = 6, 92% / 8, 9% = 0, 77
Na základě informací si vyberete akcie ABC a XYZ, které chcete investovat, protože mají nejnižší variační koeficient.
Vysvětlení
Protože variační koeficient je měřítkem rizika, pomáhá měřit volatilitu cen akcií a jiných finančních nástrojů. Pomáhá také investorům a analytikům porovnávat rizika spojená s různými potenciálními investicemi.
Variační koeficient je podobný standardní odchylce, ale standardní odchylku dvou proměnných nelze užitečně porovnat. Ale s použitím směrodatné odchylky a střední hodnoty je relativní srovnání významnější. Existuje také omezení variačního koeficientu. Předpokládejme, že průměr sady dat je nula. V takovém případě se tento nástroj stane neúčinným. Nejen to, pokud máme soubor dat, který má mnoho kladných a záporných hodnot, koeficient variace se stává velmi problematickým. Je tedy užitečnější pouze u datových sad se stejným znaménkem plus-mínus.
Relevance a použití variačního koeficientu
Variační koeficient má význam v mnoha jiných oblastech, než je statistika. Například v oblasti financí je variační koeficient měřítkem rizika. Je to podobné standardní odchylce, protože se také používá jako míra rizika, ale rozdíl je v tom, že variační koeficient je lepším ukazatelem relativního rizika. Řekněme například očekávaný výnos A 15% a očekávaný návrat B 10% a A má standardní odchylku 10%, zatímco B má standardní odchylku 5%. Pro výběr lepší investice lze použít variační koeficient. Takže variační koeficient A je 10/15 = 0, 666 a variační koeficient B je 5/10 = 0, 5. Takže B je lepší investice než A.
Doporučené články
Toto byl průvodce formulací koeficientu variací. Zde diskutujeme, jak vypočítat variační koeficient pomocí vzorce spolu s praktickými příklady a stahovatelnou šablonou Excel. Další informace naleznete také v následujících článcích -
- Co je upravený vzorec R na druhou?
- Příklady vzorce stanovení koeficientu
- Jak vypočítat korelační koeficient pomocí vzorce?
- Covariance vzorec s šablonou Excel