
Vzorec složené roční míry růstu (obsah)
- Vzorec
- Příklady
- Kalkulačka
Co je složený vzorec roční míry růstu?
Složení je účinek, kdy investice získá úrok nejen z hlavní složky, ale také z úroku. Složená roční míra růstu je tedy skutečným ročním růstem dosaženým z investic, přičemž se uvažuje o sloučení do obrazu. To v zásadě předpokládá, že úrok získaný každý rok je reinvestován a získá stejný úrok jako částka jistiny. To je důvod, proč je složená roční míra růstu vždy vyšší než jednoduchá úroková míra. Mnoho investic, jako jsou podílové fondy, návratnost akciového trhu, není příliš lineární a velmi nestabilní.
Složená roční míra růstu pomáhá při vyrovnání tohoto výnosu a řekne, kolik investor vydělal za dobu investice, vzhledem k tomu, že všechny výnosy mezi tímto obdobím jsou reinvestovány stejnou rychlostí. Díky tomuto efektu vyhlazování nám pomáhá při porovnávání datových sad s různou úrovní volatility. Velmi často se používá pro účely finanční analýzy.
Konečná částka investice = Počáteční částka (1 + CAGR) Počet let
Vzorec pro složenou roční míru růstu -
CAGR = (Ending Investment Amount / Start Amount) (1 / Number of Years) – 1
Tento vzorec je použitelný, pokud se investice každoročně kombinuje, to znamená, že peníze investujeme každoročně. Ale někdy se stává, že chceme vypočítat rychlost, ve které se slučování děje na čtvrtletní, měsíční, denní bázi. K tomu používáme níže uvedený vzorec:
Konečná částka investice = počáteční částka (1 + CAGR / složená frekvence) (počet let * složená frekvence)
Vzorec pro složenou roční míru růstu -
CAGR = Compounding Frequency * ((Ending Investment Amount / Start Amount) (1 / (Number of Years * Compounding Frequency)) – 1)
Frekvenční složení:
- Pololetní složení: 2
- Čtvrtletní složení: 4
- Měsíční frekvence: 12 a tak dále
Příklady vzorce CAGR (se šablonou Excel)
Vezměme si příklad, abychom lépe porozuměli výpočtu vzorce CAGR.
Tuto šablonu složeného ročního tempa růstu Excel si můžete stáhnout zde - šablonu složeného ročního tempa růstu ExcelVzorec CAGR - Příklad č. 1
Řekněme, že jste investovali 1 000 USD do podílových fondů před 3 lety. Následuje návrat, který jste získali za tyto 3 roky:
- 1. rok jste získali 20% nárůst hodnoty. Na konci prvního roku je tedy celková hodnota 1200 USD
- 2. rok jste získali 10% nárůst hodnoty. Na konci druhého roku je tedy celková hodnota 1320 $
- 3. rok jste získali 10% nárůst hodnoty. Na konci 3. roku je tedy celková hodnota 1452 $
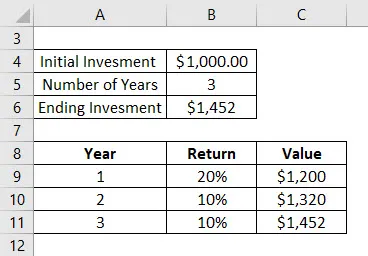
CAGR se počítá pomocí vzorce uvedeného níže
CAGR = (Konečná částka investice / počáteční částka) (1 / počet let) - 1
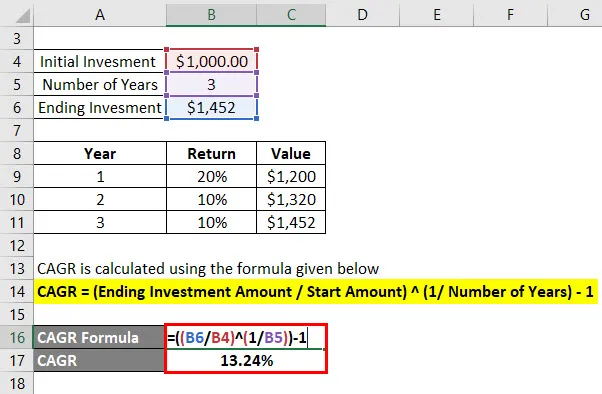
- CAGR = (1 452 $ / 1 000 $) (1/3) - 1
- CAGR = 13, 24%
Zde vidíme, že roční výnos za všechny 3 roky je odlišný a liší se, ale složená roční míra růstu nám dává jednotnou míru, kterou můžeme porovnat s různými investičními příležitostmi.
Vzorec CAGR - Příklad č. 2
Řekněme, že jste do banky investovali 1 000 $ a chcete peníze v bance ponechat po dobu 4 let. Nyní řekněme, že celková částka, kterou získáte po 4 letech, je 2 500 $. Banka nabízí sazbu s měsíčním složením. Vypočítejte CAGR.
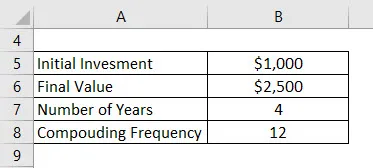
CAGR se počítá pomocí vzorce uvedeného níže
CAGR = Frekvenční složení * ((Konečná investiční částka / Počáteční částka) (1 / (Počet let * Frekvenční složení)) - 1)
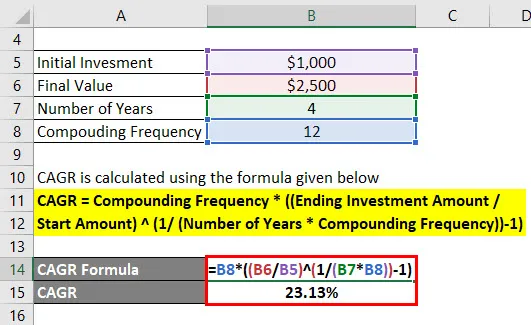
- CAGR = 12 * ((2 500 $ / 1 000 $) (1 / (4 * 12)) - 1)
- CAGR = 23, 13%
Složená roční míra růstu je tedy 23, 13%.
Vysvětlení vzorce složené roční míry růstu
Ačkoli složená roční míra růstu je roční míra investice, je to pouze teoretická hodnota a nejedná se o skutečnou návratnost. Hlavním předpokladem je, že všechny výnosy se znovu investují se stejnou sazbou pro investiční období, ale sazba nezůstane po všechny roky a my nemůžeme investovat své peníze stejným tempem. Jedná se tedy o jedinou reprezentativní sazbu, která nám říká, že s čím bychom mohli skončit, pokud budou všechny peníze reinvestovány na konci každého roku za tuto sazbu. Při použití složené roční míry růstu bychom tedy měli vzít v úvahu některé klíčové body.
Také budeme opravdu opatrní ohledně investice, která je dlouhodobá. Například, pokud je investiční období velmi dlouhé, řekněme 20 let, složená roční úroková sazba by nám mohla poskytnout nesprávný náznak, protože se může stát, že během prvních 15 let nezískáme žádný zisk a všechny výnosy se vrátí v posledním období . Vydělávat žádné zisky po dobu 15 let není přípustné pro jakoukoli firmu, aby si ji udržela.
Podobně, pokud dvě investiční příležitosti mají stejnou CAGR, může se stát, že jedna je přitahována více než druhá z důvodu důvodu, že k růstu jedné dojde v počátečním období, zatímco u druhé je soustředěna na konci doba.
Relevance a použití kombinovaného vzorce roční míry růstu
Složená roční míra růstu je skutečně užitečná při výpočtu průměrné míry růstu investice a může pomoci při srovnávání různých investic. Jak jsme viděli ve výše uvedeném příkladu, meziroční růst investic je nerovnoměrný a nevyrovnaný. Ale pomocí složené roční míry růstu se návratnost vyhlazuje. Dalším faktorem, který činí složenou roční míru růstu kritickou metodou při určování růstu investice, je to, že bere v úvahu složený účinek, který roční míra návratnosti ne. Složená roční sazba nám nedává skutečný obraz návratnosti, protože pouze vypočítává návratnost jistiny a ignoruje úroky z úrokové složky, ale není tomu tak u složené roční míry růstu.
Kalkulačka složené roční míry růstu
Můžete použít následující složenou roční kalkulačku míry růstu
| Konečná částka investice | |
| Počáteční částka | |
| Počet let | |
| CAGR | |
| CAGR = | ((Konečná částka investice / počáteční částka) 1 / počet let -1) |
| = | ((0/0) 1/0 -1) = 0 |
Doporučené články
Toto byl průvodce formulací složené roční míry růstu. Zde diskutujeme o tom, jak vypočítat CAGR, spolu s praktickými příklady. Poskytujeme také kalkulačku složeného ročního růstu s šablonou Excel ke stažení. Další informace naleznete také v následujících článcích -
- Průvodce pro výpočet míry návratnosti
- Příklady vzorce exponenciálního růstu
- Kalkulačka pro formule centrální limitní věty
- Jak vypočítat kapitalizaci trhu?