
Střední formule (obsah)
- Střední formule
- Příklady průměrného vzorce (se šablonou Excel)
- Průměrná kalkulačka vzorců
Střední formule
Průměr je bod v datové sadě, což je průměr ze všech datových bodů, které máme v sadě. Je to v podstatě aritmetický průměr datové sady a lze jej vypočítat součtem všech datových bodů a poté dělením počtem datových bodů, které máme v datové sadě. Ve statistice je průměr nejčastější metodou měření středu datové sady. Je to velmi základní, ale důležitá součást statistické analýzy dat. Pokud vypočítáme průměrnou hodnotu souboru obyvatel, pak se to nazývá průměr populace. Ale někdy se stane, že údaje o populaci jsou velmi obrovské a nemůžeme provést analýzu na tomto datovém souboru. V takovém případě z něj odebereme vzorek a vezmeme průměr. Tento vzorek v podstatě představuje soubor populace a průměr se nazývá průměr vzorku. Průměrná hodnota je průměrná hodnota, která bude klesat mezi maximální a minimální hodnotou v sadě dat, ale nebude to číslo v sadě dat.
Vzorec pro průměr je dán:
Mean = Sum of All Data Points / Number of Data Points
Existuje další způsob výpočtu průměru, který se příliš nepoužívá. Říká se tomu metoda předpokládané střední hodnoty. V této metodě je náhodná hodnota vybrána ze souboru dat a je považována za střední. Poté se vypočte odchylka datových bodů od této hodnoty. Průměr je dán:
Mean = Assumed Mean + (Sum of All Deviations / Number of Data Points)
Příklady průměrného vzorce (se šablonou Excel)
Vezměme si příklad, abychom lépe porozuměli výpočtu průměrného vzorce.
Tuto střední verzi si můžete stáhnout zde - střední šablonuStřední vzorec - příklad č. 1
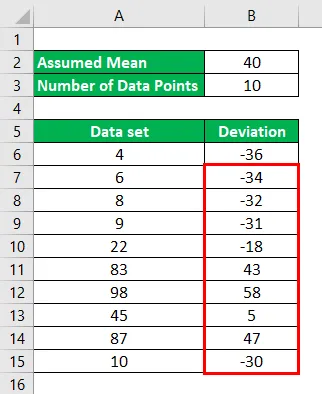
Řekněme, že máte sadu dat s 10 datovými body a my za to chceme vypočítat průměr.
Soubor dat: (4, 6, 8, 9, 22, 83, 98, 45, 87, 10)
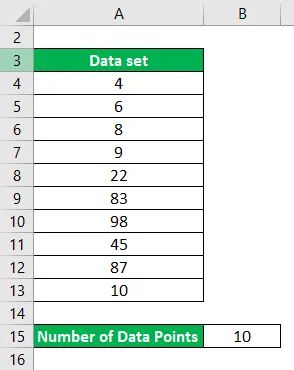
Řešení:
Průměr se vypočítá pomocí vzorce uvedeného níže
Průměr = součet všech datových bodů / počet datových bodů
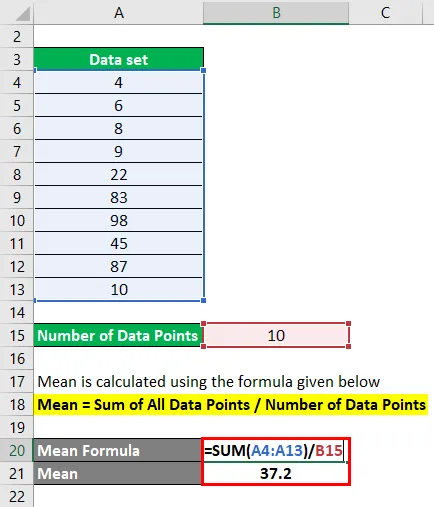
- Průměr = (4 + 6 + 8 + 9 + 22 + 83 + 98 + 45 + 87 + 10) / 10
- Průměr = 372/10
- Průměr = 37, 2
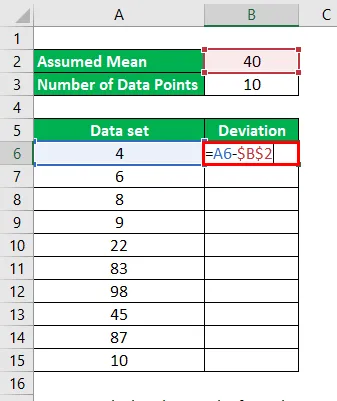
Pojďme použít metodu předpokládaného průměru k nalezení střední hodnoty ve stejném příkladu.
Předpokládejme, že průměr pro daný datový soubor je 40. Takže odchylky budou počítány jako:
Pro 1. datový bod, 4 - 40 = -36
Výsledek bude uveden níže.
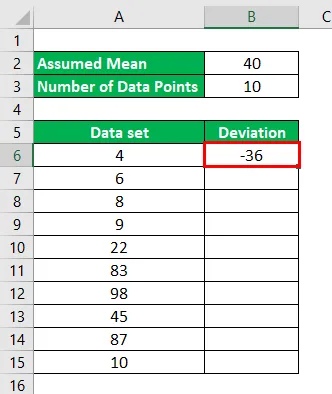
Podobně musíme vypočítat odchylku pro všechny datové body.
Průměr se vypočítá pomocí vzorce uvedeného níže
Průměr = předpokládaný průměr + (součet všech odchylek / počet datových bodů)
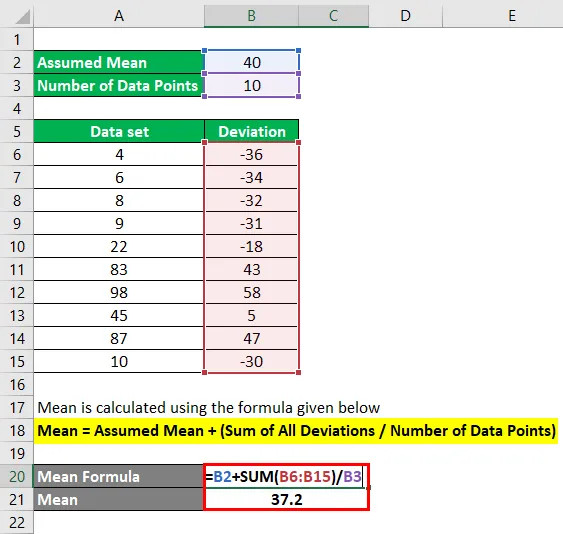
- Průměr = 40 + (-36 -34-32-31-18 + 43 + 58 + 5 + 47-30) / 10
- Průměr = 40 + (-28) / 10
- Průměr = 40 + (-2, 8)
- Průměr = 37, 2
Střední vzorec - Příklad č. 2
Vezměme si zásoby IBM a vezmeme její historické ceny z posledních 10 měsíců a vypočítáme roční výnos za 10 měsíců.
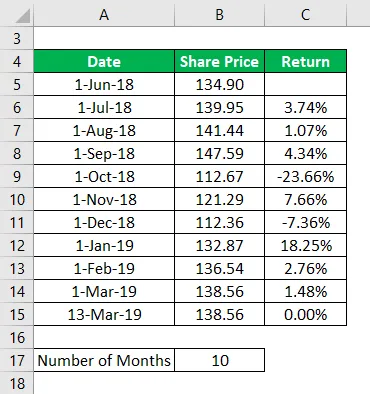
Zdrojový odkaz: https://in.finance.yahoo.com/quote/IBM/
Řešení:
Průměr se vypočítá pomocí vzorce uvedeného níže
Průměr = součet všech datových bodů / počet datových bodů
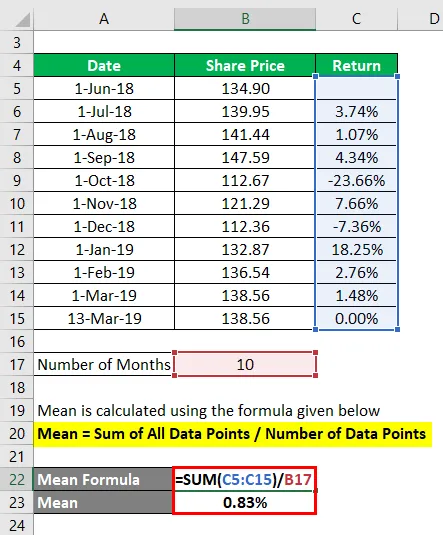
- Průměr = (3, 74% + 1, 07% + 4, 34% + (-23, 66)% + 7, 66% + (-7, 36)% + 18, 25% + 2, 76% + 1, 48% + 0, 00%) / 10
- Průměr = 8, 28% / 10
- Průměr = 0, 83%
Takže pokud zde vidíte, za posledních 10 měsíců se návratnost IBM velmi pohybovala.
Celkově je průměrný výnos za posledních 10 měsíců pouze 0, 83%
Vysvětlení
Průměr je v podstatě jednoduchý průměr datových bodů, které máme v datové sadě, a pomáhá nám to pochopit průměrný bod datové sady. Existují však určitá omezení, pokud jde o použití střední hodnoty. Střední hodnota je snadno zkreslena extrémními hodnotami / extrémními hodnotami. Tyto extrémní hodnoty mohou být velmi malé nebo velmi velké hodnoty, které mohou zkreslit průměr. Například: Řekněme, že máme výnosy zásob za posledních 5 let dané 5%, 2%, 1%, 5%, -30%. Průměr pro tyto hodnoty je -3, 4% ((5 + 2 + 1 + 5-30) / 5). Ačkoliv akcie dosáhly kladných výnosů za první 4 roky, v průměru máme záporný průměr 3, 4%. Podobně, pokud máme projekt, pro který analyzujeme peněžní tok pro následujících 5 let. Řekněme, že peněžní toky jsou: -100, -100, -100, -100, +1000.
Průměr je 600/5 = 120. Přestože máme pozitivní průměr, dostáváme peníze pouze v posledním roce projektu a může se stát, že pokud začleníme časovou hodnotu peněz, nebude tento projekt vypadat tak lukrativně, jak je nyní .
Relevance a použití průměrného vzorce
Průměr je velmi jednoduchý, přesto je jedním z klíčových prvků statistiky. Je základním základem statistické analýzy dat. Je velmi snadné spočítat a také snadno pochopit. Pokud máme sadu dat s datovými body, které jsou rozptýleny všude, znamená to, že nám pomáhá zjistit, jaký je průměr daného datového bodu. Například: Pokud má akcie X výnosy z posledních 5 let jako 20%, -10%, 3%, -7%, 30%. Pokud vidíte, všechny roky mají různé výnosy. Průměrná hodnota pro toto je 7, 2% ((20-10 + 3-7 + 30) / 5). Můžeme nyní jednoduše říci, že v průměru nám akcie daly roční výnos 7, 2%.
Pokud ale v silach vidíme průměr, má to relativně menší význam z důvodu výše diskutovaných vad a je to spíše teoretické číslo. Měli bychom tedy používat střední hodnotu velmi opatrně a neměli bychom analyzovat data pouze na základě střední hodnoty.
Průměrná kalkulačka vzorců
Můžete použít následující střední kalkulačku
| Součet všech datových bodů | |
| Počet datových bodů | |
| Střední formule | |
| Střední formule | = |
|
|
Doporučené články
Toto byl průvodce průměrným vzorcem. Zde diskutujeme o tom, jak vypočítat střední hodnotu, spolu s praktickými příklady. Poskytujeme také střední kalkulačku se stahovatelnou šablonou Excel. Další informace naleznete také v následujících článcích -
- Výpočet cenové elasticity
- Průvodce po vzorci koeficientu solventnosti
- Příklady vzorce portfolia
- Vzorec DPMO