Úvod do funkce Sum v Matlabu

MATLAB je jazyk používaný pro technické výpočty. Jak většina z nás bude souhlasit, snadno použitelné prostředí je nutností pro integraci úkolů výpočetní techniky, vizualizace a konečně programování. MATLAB dělá totéž tím, že poskytuje prostředí, které je nejen snadno použitelné, ale také řešení, která dostáváme, jsou zobrazena v podobě matematických zápisů, které většina z nás zná. V tomto článku se podrobně podíváme na funkci Sum v Matlabu.

Použití Matlabu zahrnout (ale neomezeno na)

  • Výpočet
  • Vývoj algoritmů
  • Modelování
  • Simulace
  • Prototypování
  • Analytika dat (analýza a vizualizace dat)
  • Inženýrská a vědecká grafika
  • Vývoj aplikací

MATLAB poskytuje svému uživateli košík funkcí, v tomto článku budeme rozumět výkonné funkci nazvané 'Sum funkce'.

Syntax:

S = sum(A)

S = sum(A, dim)

S = sum(A, vecdim)

S = sum(__, outtype)

S = sum(__, nanflag)

Popis funkce Sum v Matlabu

Nyní pochopíme všechny tyto funkce jeden po druhém.

1. S = součet (A)

  • Tím se vrátí součet všech prvků 'A' podél dimenze pole, které není singleton, tj. Velikost není rovna 1 (Bude se brát v úvahu první dimenze, která není singleton).
  • suma (A) vrátí součet prvků, pokud A je vektor.
  • suma (A) vrátí vektor řádků, který bude mít některé z každého sloupce, pokud A je matice.
  • Pokud A je vícerozměrné pole, součet (A) bude fungovat podél dimenze 1. pole, jehož velikost není rovna 1 a bude se všemi prvky zacházet jako s vektory. Tato dimenze bude 1 a velikost ostatních dimenzí se nezmění.

Nyní chápeme součet (A) s příkladem. Předtím však mějte na paměti, že v MATLABu mají matice následující rozměry:

1 = řádky, 2 = sloupce, 3 = hloubka

Příklad č. 1 - Když máme oba řádky a sloupce

Jak je vysvětleno výše, součet (A) provede sčítání podél 1. dimenze, která není singleton. Pro jeden řádek / sloupec dostaneme výsledek jako jedno číslo.

A = (1, 3, 7 ; 5, -8, 1);
S = sum(A);

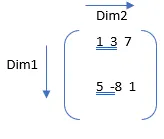
Poznámka : zde S je výsledný součet a A je pole, jehož součet potřebujeme. A =

Zde 1 je první nes singletonový rozměr (rozměr, jehož délka není rovna 1). Některé budou tedy spolu s prvky řady, tj. Klesat.

S = součet (A) = 6 -5 8

Příklad č. 2 - Když máme pouze 1 řádek

A = (2, 3, 7 );
B = sum(A);

Zde je první ne singletonová dimenze 2 (tj. Sloupce). Součet bude tedy spolu s prvky sloupce

B = součet (A) = 12

Příklad č. 3 - Když máme pouze 1 sloupec

A = (2 ; 5);

Takže A =

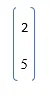
Zde je první nes singletonová dimenze 1, takže součet bude spolu s prvky řady.

B = součet (A) = 7

2. S = součet (A, dim)

Tato funkce vrátí součet podél dimenze předané v argumentu.

Příklad

A = (2 4 3; 5 3 6; 7 2 5)

Takže A =

S = součet (A, 2)

Zde jsme jako argument předali „2“, takže součet bude podél dimenze 2.
Takže S =

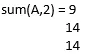
3. S = součet (A, vecdim)

Tato funkce sčítá prvky na základě rozměrů, které jsou uvedeny ve vektoru „vecdim“. Např. pokud máme matici, pak součet (A, (1 2)) bude součtem všech prvků v A, protože každý prvek matice A bude obsažen v řezu pole definovaném rozměry 1 a 2 ( Pamatujte, že dimenze 1 je pro řádky a 2 pro sloupce)

Příklad

A = ones(3, 3, 2); (Tím se vytvoří pole 3D, jehož všechny prvky jsou rovny 1)

Nyní, Abychom sčítali všechny prvky přítomné v každém řezu matice A, musíme určit rozměry, které chceme sčítat (řádek i sloupec). To můžeme udělat poskytnutím vektorové dimenze jako argumentu. V našem příkladu jsou oba řezy maticí 3 * 3, takže součet bude 9.

S1 = součet (A, (1 2))
S1 = S1 (:, :, 1) = 9
&
S1 (:, :, 2) = 9

4. S = součet (A, outtype)

Tato funkce vrátí součet s typem dat předaným v argumentu. „Outtyp“ může být „nativní“, „výchozí“ nebo „dvojitý“.

Příklad

A = int32(5: 10);
S = sum(A, 'native')

Výstupem pro to bude,

S = int32
45

Kde int32 je nativní datový typ prvků A a 45 je součet prvků od 5 do 10.

5. S = suma (nanflag)

Tím se určí, zda z našich výpočtů musíme zahrnout nebo vynechat NaN.

součet (A, 'includeenan') bude zahrnovat všechny hodnoty NaN, které jsou přítomny ve výpočtu.

suma (A, 'omitnan') bude ignorovat všechny hodnoty NaN.

Příklad

A = (1 -5 3 -2 NaN 4 NaN 9);
S = sum(A, 'omitnan')

Takže výstup, který dostaneme, je
S = 10
(Po ignorování všech hodnot NaN)

Závěr

Jak tedy vidíme, MATLAB je systém, jehož základním datovým prvkem je pole, které nevyžaduje žádné kótování. To nám umožňuje řešit počítačové problémy, zejména problémy s maticovými a vektorovými formulacemi. To vše se děje za výrazně kratší dobu ve srovnání s psaním programu ve skalárním a neinteraktivním jazyce, jako je C.

Doporučené články

Toto je průvodce funkcí Sum Sum v Matlabu. Zde diskutujeme použití Matlabu, syntaxi, příklady spolu s popisem funkce sum v Matlabu. Další informace naleznete také v následujících článcích

  1. Vektory v Matlabu
  2. Přenos funkcí v Matlabu
  3. Operátory Matlab
  4. Co je Matlab?
  5. Kompilátor Matlab | Aplikace Matlab Compiler

Kategorie:

Velká data