
F-testovací vzorec (obsah)
- Vzorec
- Příklady
Co je F-Test Formula?
F-test je statistický test, který nám pomáhá při zjišťování, zda dvě sady populace, které mají normální distribuci svých datových bodů, mají stejnou standardní odchylku nebo odchylku. Ale první a nejpřednější věc pro provedení F-testu je to, že soubory dat by měly mít normální distribuci. Toto je aplikováno na distribuci F pod nulovou hypotézou. F-test je velmi důležitou součástí analýzy variace (ANOVA) a je vypočítán na základě poměrů dvou variací dvou různých datových souborů. Jak víme, tyto odchylky nám poskytují informace o rozptylu datových bodů. F-test se také používá v různých testech, jako je regresní analýza, Chow test atd.
Vzorec pro F-test:
Pro F-Test neexistuje jednoduchý vzorec, ale je to řada kroků, které musíme následovat:
Krok 1: K provedení F-testu musíme nejprve definovat nulovou hypotézu a alternativní hypotézu. Jsou dány: -
- H0 (nulová hypotéza): Variace 1. sady dat = Variace 2. sady dat
- Ha: Variace 1. sady dat <Variace 2. sady dat (pro dolní jednostranný test)
- Ha: Variace 1. datové sady> Varianta 2. datové sady (pro horní jednostranný test)
- Ha: Varianta 1. datové sady ≠ Varianta 2. datové sady (pro dvoustranný test)
Krok 2: Další věcí, kterou musíme udělat, je, že musíme zjistit úroveň významnosti a poté určit stupně volnosti čitatele i jmenovatele. To nám pomáhá při určování jejich kritických hodnot. Stupeň volnosti je velikost vzorku -1.
Krok 3: F-testovací vzorec:
F Value = Variance of 1 st Data Set / Variance of 2 nd Data Set
Krok 4: Najděte kritickou hodnotu F z tabulky F s mírou volnosti a úrovně významnosti.
Krok 5: Porovnejte tyto dvě hodnoty a pokud je kritická hodnota menší než hodnota F, můžete odmítnout nulovou hypotézu.
Příklady vzorce F-Test (se šablonou Excel)
Vezměme si příklad, abychom lépe porozuměli výpočtu F-testu.
Tuto šablonu F-TEST Formula Excel si můžete stáhnout zde - F-TEST Formula Excel ExcelF-testovací vzorec - příklad č. 1
Řekněme, že máme dvě datové sady A a B, které obsahují různé datové body. Proveďte F-test a určete, zda můžeme nulovou hypotézu odmítnout na 1% hladině významnosti.
Sady dat:
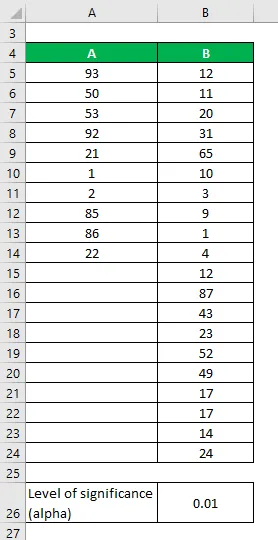
Řešení:
Nulová hypotéza: Varianta A = Varianta B
Stupeň svobody se počítá jako
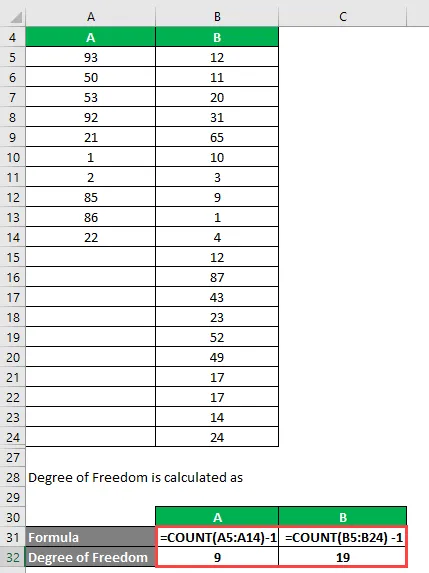
Stupeň svobody
- Pro A = 10 - 1 = 9
- Pro B = 20 - 1 = 19
Variace se počítá jako:

- Varianta A = 1385, 61
- Varianta B = 521, 22
F Hodnota se vypočítá pomocí vzorce uvedeného níže
F Hodnota = Variace 1. sady dat / Variace 2. sady dat
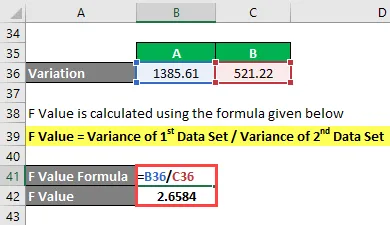
- F Hodnota = 1385, 61 / 521, 22
- F Hodnota = 2, 6584
F-tabulka:
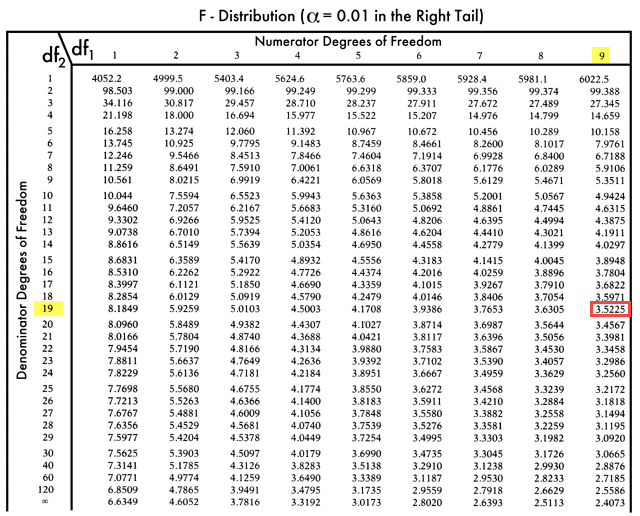
Kritická hodnota F = 3, 5225
Protože Friticita je větší než hodnota F, nemůžeme odmítnout nulovou hypotézu.
F-testovací vzorec - Příklad č. 2
Předpokládejme, že pracujete ve výzkumné společnosti a chcete, aby se úroveň emisí oxidu uhličitého dělala ze 2 různých značek cigaret a zda se výrazně liší nebo ne. Ve své analýze jste shromáždili následující informace:
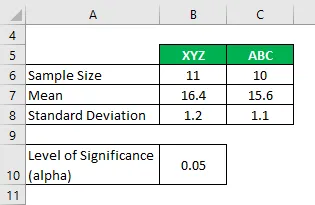
Řešení:
Stupeň svobody se počítá jako
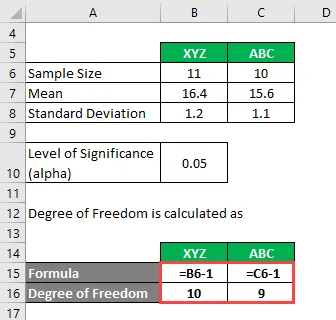
Stupeň svobody
- Pro XYZ = 11 - 1 = 10
- Pro ABC = 10 - 1 = 9
Variace se počítá jako:
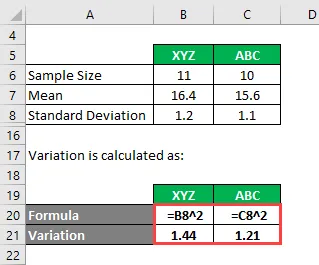
- Varianta XYZ = 1, 2 2 = 1, 44
- Varianta ABC = 1, 1 2 = 1, 21
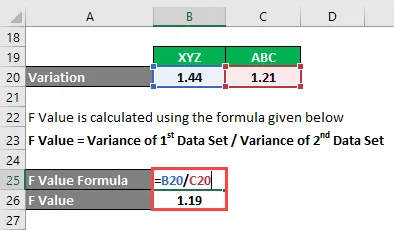
- F Hodnota = 1, 44 / 1, 21
- Hodnota F = 1, 19
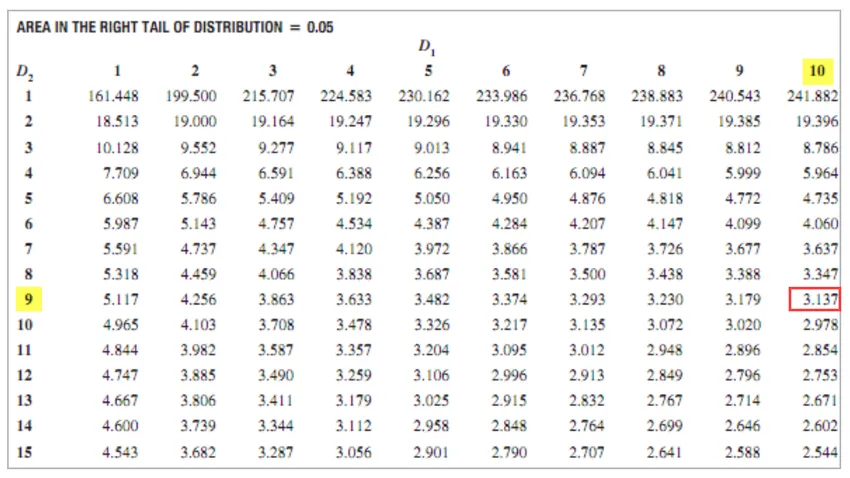
F Kritická hodnota = 3, 137
Protože hodnota F kritická> F nelze nulovou hypotézu odmítnout.
Vysvětlení
Ve výše uvedených příkladech jsme viděli aplikaci F-testu a jak se provádí. Existuje však řada předpokladů, které musíme před provedením F-testu postarat, jinak nedostaneme požadované výsledky:
- První věc je, že při výpočtu hodnoty F musíme vždy umístit čitatel s vyšší hodnotou rozptylu. Takže pokud F = V1 / V2, V1 by měla být> V2
- Pokud chceme provést 2 ocasní test, musíme dělit hladinu významnosti 2 a to bude správná úroveň pro nalezení kritické hodnoty
- Použijeme pouze rozptyl pro výpočet hodnoty F a pokud dostaneme směrodatné odchylky, jako v příkladu 2, musíme najít druhou mocninu pro nalezení rozptylu.
- Oba vzorky by měly být na sobě nezávislé a velikost vzorku by měla být menší než 30
- Soubory populace, z nichž jsou vzorky odebírány, musí být normálně distribuovány
Toto jsou klíčové parametry / předpoklad, o který by se mělo při provádění F-testu jednat.
Relevance a použití vzorce F-testu
F-Test, jak jsme diskutovali výše, nám pomáhá kontrolovat rovnost dvou variací populace. Takže když máme dva nezávislé vzorky, které jsou odebrány z normální populace a chceme zkontrolovat, zda mají stejnou variabilitu, použijeme F-test. F-test má také velký význam v regresní analýze a také pro testování významnosti R2. Stručně řečeno, F-Test je velmi důležitým nástrojem ve statistice, pokud chceme porovnat variace 2 nebo více datových sad. Před provedením tohoto testu je však třeba mít na paměti všechny předpoklady.
Doporučené články
Toto byl průvodce F-testovacím vzorcem. Zde diskutujeme o tom, jak vypočítat F-test, spolu s praktickými příklady a šablonou Excel ke stažení. Další informace naleznete také v následujících článcích -
- T Distribuční vzorec
- Vzorec pro stanovení ceny dluhopisů
- Procentuální chyba vzorec
- Výpočet vzorce NOPAT